Linear Regression
Dr. D’Agostino McGowan
Lab follow-up
- Knit, commit, and push after every exercise
- When you are working on labs, homeworks, or application exercises, edit the file I have started for you (
01-hello-r.Rmd) - Any questions?
Linear Models
- Go to the sta-363-s20 GitHub organization and search for
appex-01-linear-models - Clone this repository into RStudio Cloud
Linear Regression Questions
- Is there a relationship between a response variable and predictors?
- How strong is the relationship?
- What is the uncertainty?
- How accurately can we predict a future outcome?
Simple linear regression
Y=β0+β1X+ϵ
Simple linear regression
Y=β0+β1X+ϵ
- β0: intercept
Simple linear regression
Y=β0+β1X+ϵ
- β0: intercept
- β1: slope
Simple linear regression
Y=β0+β1X+ϵ
- β0: intercept
- β1: slope
- β0 and β1 are coefficients, parameters
Simple linear regression
Y=β0+β1X+ϵ
- β0: intercept
- β1: slope
- β0 and β1 are coefficients, parameters
- ϵ: error
Simple linear regression
We estimate this with
^y=^β0+^β1x
Simple linear regression
We estimate this with
^y=^β0+^β1x
- ^y is the prediction of Y when X=x
Simple linear regression
We estimate this with
^y=^β0+^β1x
- ^y is the prediction of Y when X=x
- The hat denotes that this is an estimated value

Simple linear regression
Yi=β0+β1Xi+ϵi
ϵi∼N(0,σ2)
Simple linear regression
Yi=β0+β1Xi+ϵi
ϵi∼N(0,σ2)
Y1=β0+β1X1+ϵ1Y2=β0+β1X2+ϵ2⋮⋮⋮Yn=β0+β1Xn+ϵn
Simple linear regression
Yi=β0+β1Xi+ϵi
ϵi∼N(0,σ2)
Y1=β0+β1X1+ϵ1Y2=β0+β1X2+ϵ2⋮⋮⋮Yn=β0+β1Xn+ϵn
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣β0+β1X1β0+β1X2⋮β0+β1Xn⎤⎥ ⎥ ⎥ ⎥⎦+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
Yi=β0+β1Xi+ϵi
ϵi∼N(0,σ2)
Y1=β0+β1X1+ϵ1Y2=β0+β1X2+ϵ2⋮⋮⋮Yn=β0+β1Xn+ϵn
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦X: Design Matrix[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦X: Design Matrix[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
What are the dimensions of X?
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦X: Design Matrix[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
What are the dimensions of (\mathbf{X})?
- n×2
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦X: Design Matrix[β0β1]β: Vector of parameters+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦X: Design Matrix[β0β1]β: Vector of parameters+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
What are the dimensions of β?
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦ϵ: vector of error terms
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦ϵ: vector of error terms
What are the dimensions of ϵ?
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦Y: Vector of responses=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦Y: Vector of responses=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
What are the dimensions of Y?
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢⎣Y1Y2⋮Yn⎤⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1X11X2⋮⋮1Xn⎤⎥ ⎥ ⎥ ⎥⎦[β0β1]+⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦
Y=Xβ+ϵ
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢ ⎢⎣^y1^y2⋮^yn⎤⎥ ⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1x11x2⋮⋮1xn⎤⎥ ⎥ ⎥ ⎥⎦[^β0 ^β1]
^yi=^β0+^β1xi
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢ ⎢⎣^y1^y2⋮^yn⎤⎥ ⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1x11x2⋮⋮1xn⎤⎥ ⎥ ⎥ ⎥⎦[^β0 ^β1]
^yi=^β0+^β1xi
- ϵi=yi−^yi
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢ ⎢⎣^y1^y2⋮^yn⎤⎥ ⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1x11x2⋮⋮1xn⎤⎥ ⎥ ⎥ ⎥⎦[^β0 ^β1]
^yi=^β0+^β1xi
- ϵi=yi−^yi
- ϵi=yi−(^β0+^β1xi)
Simple linear regression
⎡⎢ ⎢ ⎢ ⎢ ⎢⎣^y1^y2⋮^yn⎤⎥ ⎥ ⎥ ⎥ ⎥⎦=⎡⎢ ⎢ ⎢ ⎢⎣1x11x2⋮⋮1xn⎤⎥ ⎥ ⎥ ⎥⎦[^β0 ^β1]
^yi=^β0+^β1xi
- ϵi=yi−^yi
- ϵi=yi−(^β0+^β1xi)
- ϵi is known as the residual for observation i
Simple linear regression
How are ^β0 and ^β1 chosen? What are we minimizing?
Simple linear regression
How are ^β0 and ^β1 chosen? What are we minimizing?
- Minimize the residual sum of squares
Simple linear regression
How are ^β0 and ^β1 chosen? What are we minimizing?
- Minimize the residual sum of squares
- RSS = ∑ϵ2i=ϵ21+ϵ22+⋯+ϵ2n
Simple linear regression
How could we re-write this with yi and xi?
- Minimize the residual sum of squares
- RSS = ∑ϵ2i=ϵ21+ϵ22+⋯+ϵ2n
Simple linear regression
How could we re-write this with yi and xi?
- Minimize the residual sum of squares
- RSS = ∑ϵ2i=ϵ21+ϵ22+⋯+ϵ2n
- RSS = (y1−^β0−^β1x1)2+(y2−^β0−^β1x2)2+⋯+(yn−^β0−^β1xn)2
Simple linear regression
Let's put this back in matrix form:
∑ϵ2i=[ϵ1ϵ2…ϵn]⎡⎢ ⎢ ⎢ ⎢⎣ϵ1ϵ2⋮ϵn⎤⎥ ⎥ ⎥ ⎥⎦=ϵTϵ
Simple linear regression
What can we replace ϵi with? (Hint: look back a few slides)
Simple linear regression
What can we replace ϵi with? (Hint: look back a few slides)
∑ϵ2i=(Y−Xβ)T(Y−Xβ)
Simple linear regression
OKAY! So this is the thing we are trying to minimize with respect to β:
(Y−Xβ)T(Y−Xβ)
In calculus, how do we minimize things?
Simple linear regression
OKAY! So this is the thing we are trying to minimize with respect to β:
(Y−Xβ)T(Y−Xβ)
In calculus, how do we minimize things?
- Take the derivative with respect to β
- Set it equal to 0 (or a vector of 0s!)
- Solve for β
Simple linear regression
OKAY! So this is the thing we are trying to minimize with respect to β:
(Y−Xβ)T(Y−Xβ)
In calculus, how do we minimize things?
- Take the derivative with respect to β
- Set it equal to 0 (or a vector of 0s!)
- Solve for β ddβ(Y−Xβ)T(Y−Xβ)=−2XT(Y−Xβ)
Simple linear regression
OKAY! So this is the thing we are trying to minimize with respect to β:
(Y−Xβ)T(Y−Xβ)
In calculus, how do we minimize things?
- Take the derivative with respect to β
- Set it equal to 0 (or a vector of 0s!)
- Solve for β ddβ(Y−Xβ)T(Y−Xβ)=−2XT(Y−Xβ) −2XT(Y−Xβ)=0
Simple linear regression
OKAY! So this is the thing we are trying to minimize with respect to β:
(Y−Xβ)T(Y−Xβ)
In calculus, how do we minimize things?
- Take the derivative with respect to β
- Set it equal to 0 (or a vector of 0s!)
- Solve for β ddβ(Y−Xβ)T(Y−Xβ)=−2XT(Y−Xβ) −2XT(Y−Xβ)=0 XTY=XTXβ
Simple linear regression
XTY=XTX^β
[^β0^β1]=(XTX)−1XTY
Simple linear regression
^Y=X^β^Y=X(XTX)−1XTY
Simple linear regression
^Y=X^β^Y=X(XTX)−1XTY^β
Simple linear regression
^Y=X^β^Y=X(XTX)−1XThat matrixY
Simple linear regression
^Y=X^β^Y=X(XTX)−1XThat matrixY
Why do you think this is called the "hat matrix"

Linear Models
- Go to the sta-363-s20 GitHub organization and search for
appex-01-linear-models - Clone this repository into RStudio Cloud
- Complete the exercises
- Knit, Commit, Push
- Leave RStudio Cloud open, we may return at the end of class
Multiple linear regression
We can generalize this beyond just one predictor
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣^β0^β1⋮^βp⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦=(XTX)−1XTY
Multiple linear regression
We can generalize this beyond just one predictor
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣^β0^β1⋮^βp⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦=(XTX)−1XTY
What are the dimensions of the design matrix, X now?
Multiple linear regression
We can generalize this beyond just one predictor
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣^β0^β1⋮^βp⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦=(XTX)−1XTY
What are the dimensions of the design matrix, (\mathbf{X}) now?
- Xn×(p+1)
Multiple linear regression
We can generalize this beyond just one predictor
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣^β0^β1⋮^βp⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦=(XTX)−1XTY
What are the dimensions of the design matrix, X now?
X=⎡⎢ ⎢ ⎢ ⎢ ⎢⎣1X11X12…X1p1X21X22…X2p⋮⋮⋮⋮⋮1Xn1Xn2…Xnp⎤⎥ ⎥ ⎥ ⎥ ⎥⎦
^β interpretation in multiple linear regression
^β interpretation in multiple linear regression
The coefficient for x is ^β (95% CI: LB^β,UB^β). A one-unit increase in x yields an expected increase in y of ^β, holding all other variables constant.
Linear Regression Questions
- ✔️ Is there a relationship between a response variable and predictors?
- How strong is the relationship?
- What is the uncertainty?
- How accurately can we predict a future outcome?
Linear Regression Questions
- ✔️ Is there a relationship between a response variable and predictors?
- How strong is the relationship?
- What is the uncertainty?
- How accurately can we predict a future outcome?
Linear regression uncertainty
- The standard error of an estimator reflects how it varies under repeated sampling
Linear regression uncertainty
- The standard error of an estimator reflects how it varies under repeated sampling
Var(^β)=σ2(XTX)−1
Linear regression uncertainty
- The standard error of an estimator reflects how it varies under repeated sampling
Var(^β)=σ2(XTX)−1
- σ2=Var(ϵ)
Linear regression uncertainty
- The standard error of an estimator reflects how it varies under repeated sampling
Var(^β)=σ2(XTX)−1
- σ2=Var(ϵ)* In the case of simple linear regression,
SE(^β1)2=σ2∑ni=1(xi−¯x)2
Linear regression uncertainty
- The standard error of an estimator reflects how it varies under repeated sampling
Var(^β)=σ2(XTX)−1
- σ2=Var(ϵ)* In the case of simple linear regression,
SE(^β1)2=σ2∑ni=1(xi−¯x)2
- This uncertainty is used in the test statistic t=^β1SE^β1
Let's look at an example
Let's look at a sample of 116 sparrows from Kent Island. We are intrested in the relationship between Weight and Wing Length
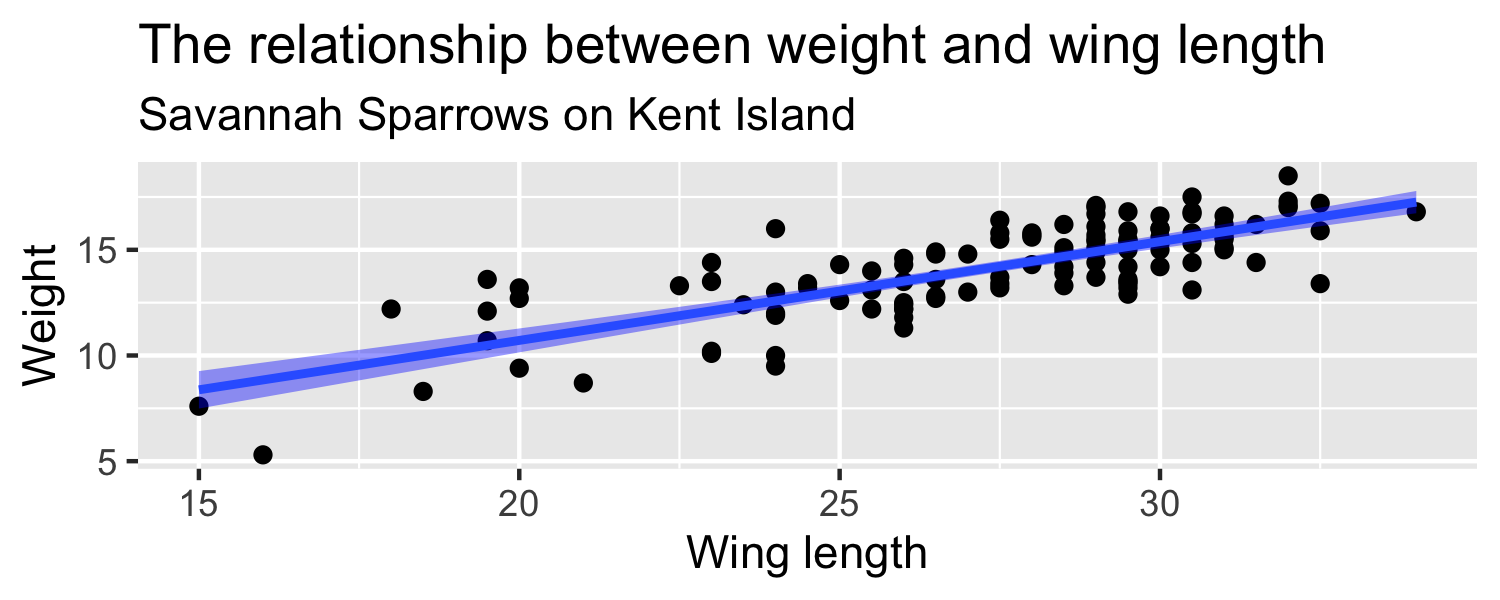
- the standard error of ^β1 ( SE^β1 ) is how much we expect the sample slope to vary from one random sample to another.
broom
a quick pause for R


- You're familiar with the tidyverse:
library(tidyverse)- The broom package takes the messy output of built-in functions in R, such as
lm, and turns them into tidy data frames.
library(broom)How does a pipe work?
- You can think about the following sequence of actions - find key, unlock car, start car, drive to school, park.
- Expressed as a set of nested functions in R pseudocode this would look like:
park(drive(start_car(find("keys")), to = "campus"))- Writing it out using pipes give it a more natural (and easier to read) structure:
find("keys") %>% start_car() %>% drive(to = "campus") %>% park()What about other arguments?
To send results to a function argument other than first one or to use the previous result for multiple arguments, use .:
starwars %>% filter(species == "Human") %>% lm(mass ~ height, data = .)## ## Call:## lm(formula = mass ~ height, data = .)## ## Coefficients:## (Intercept) height ## -116.58 1.11Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
How do we interpret this?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
How do we interpret this?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25- "the sample slope is more than 13 standard errors above a slope of zero"
Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25- confidence intervals
- p-values
Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536- confidence intervals
- p-values
Sparrows
How are these statistics distributed under the null hypothesis?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
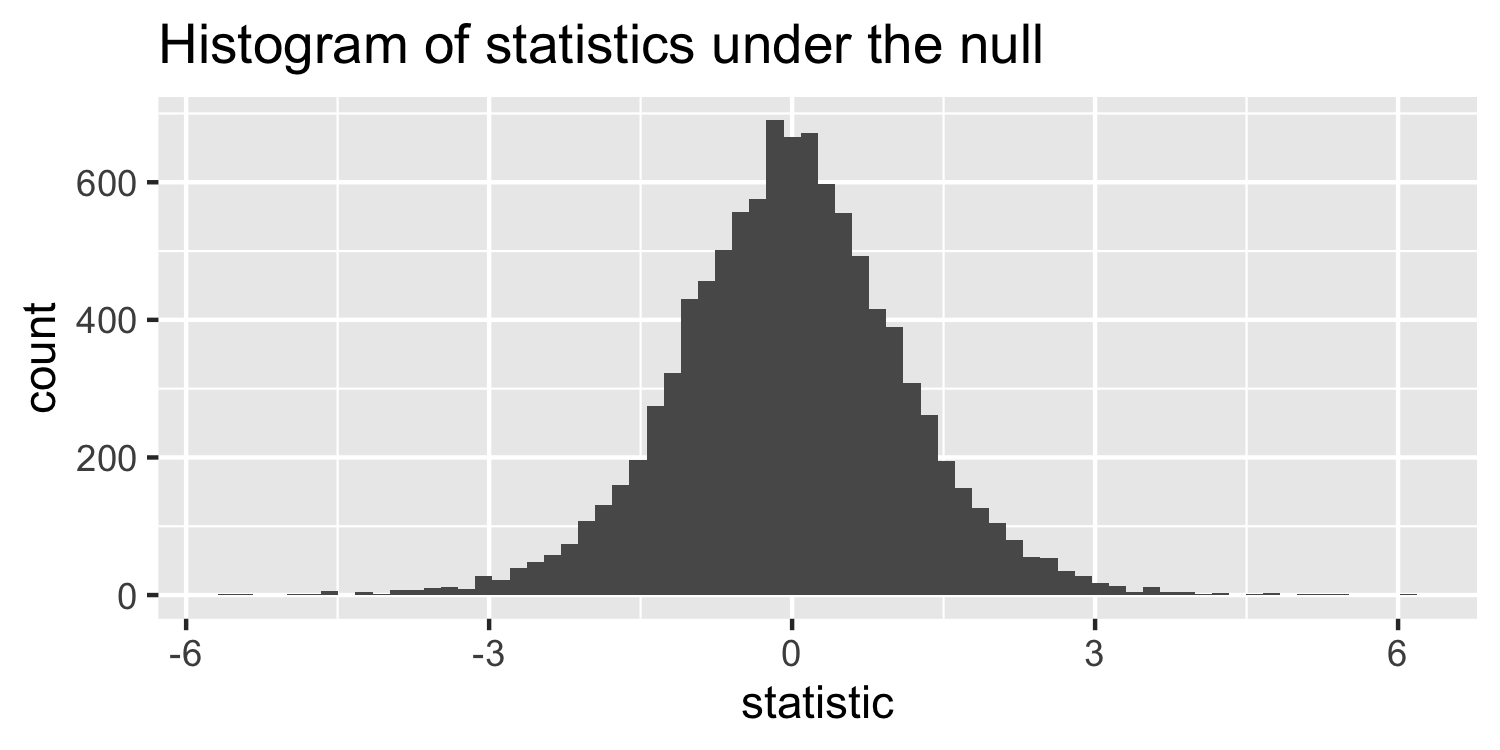
- I've generated some data under a null hypothesis where n=20
Sparrows
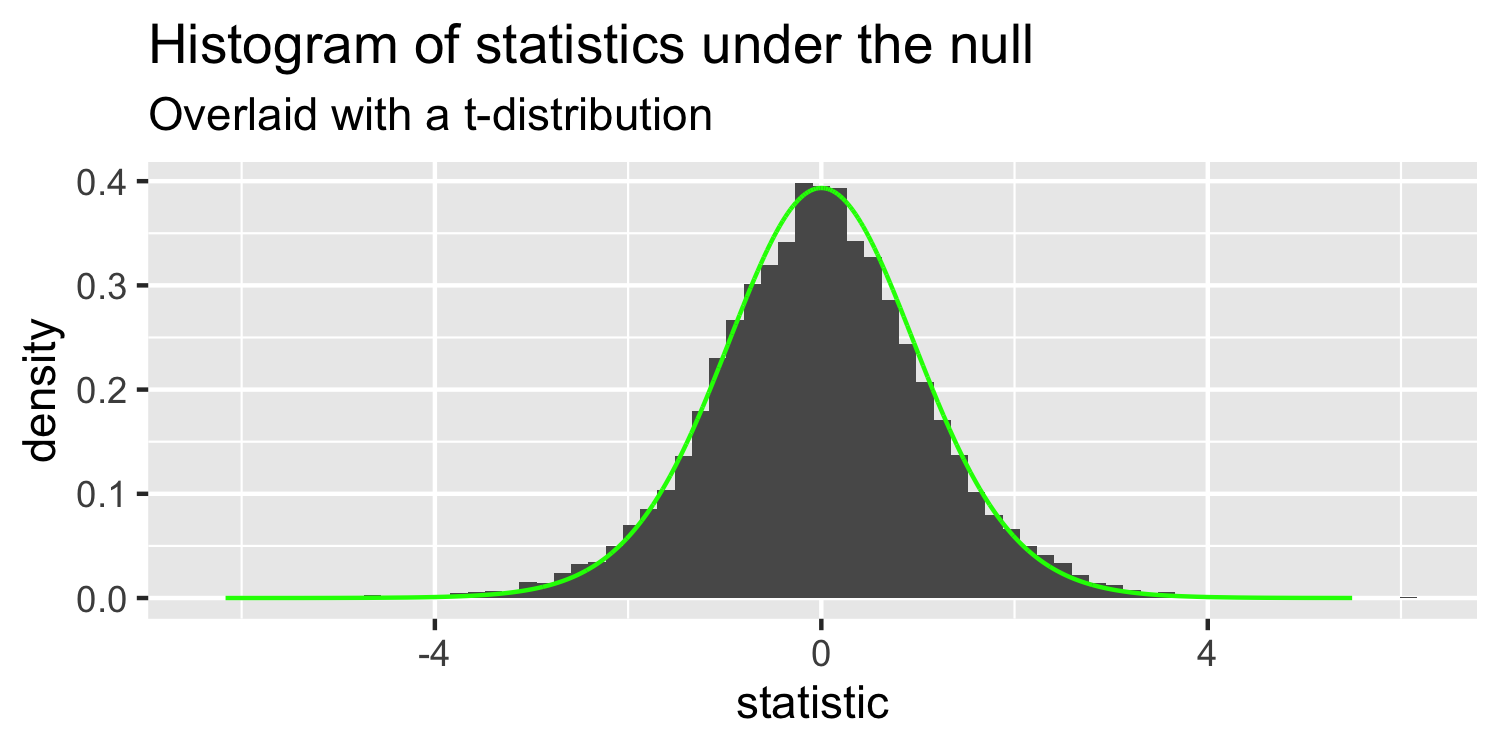
- this is a t-distribution with n-p-1 degrees of freedom.
Sparrows
The distribution of test statistics we would expect given the null hypothesis is true, β1=0, is t-distribution with n-2 degrees of freedom.
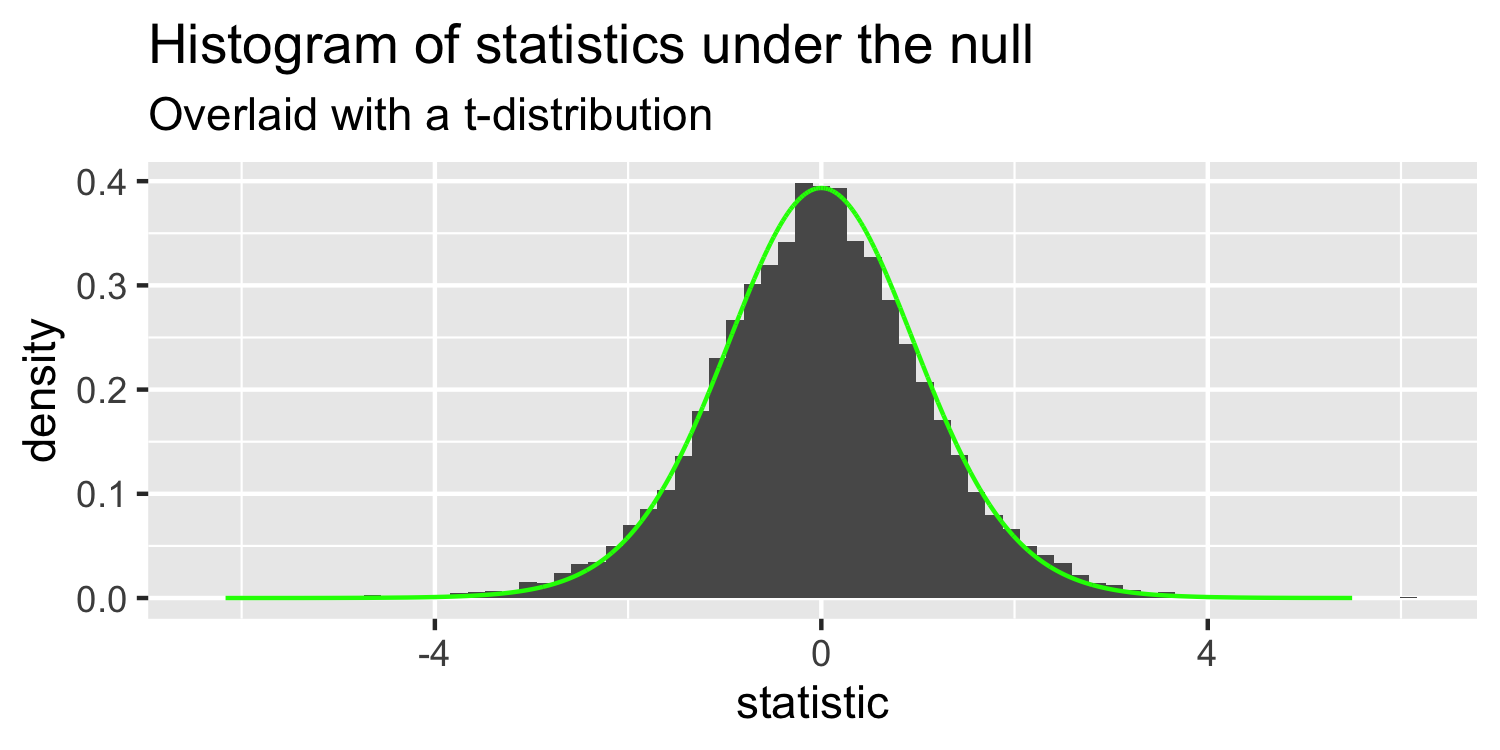
Sparrows
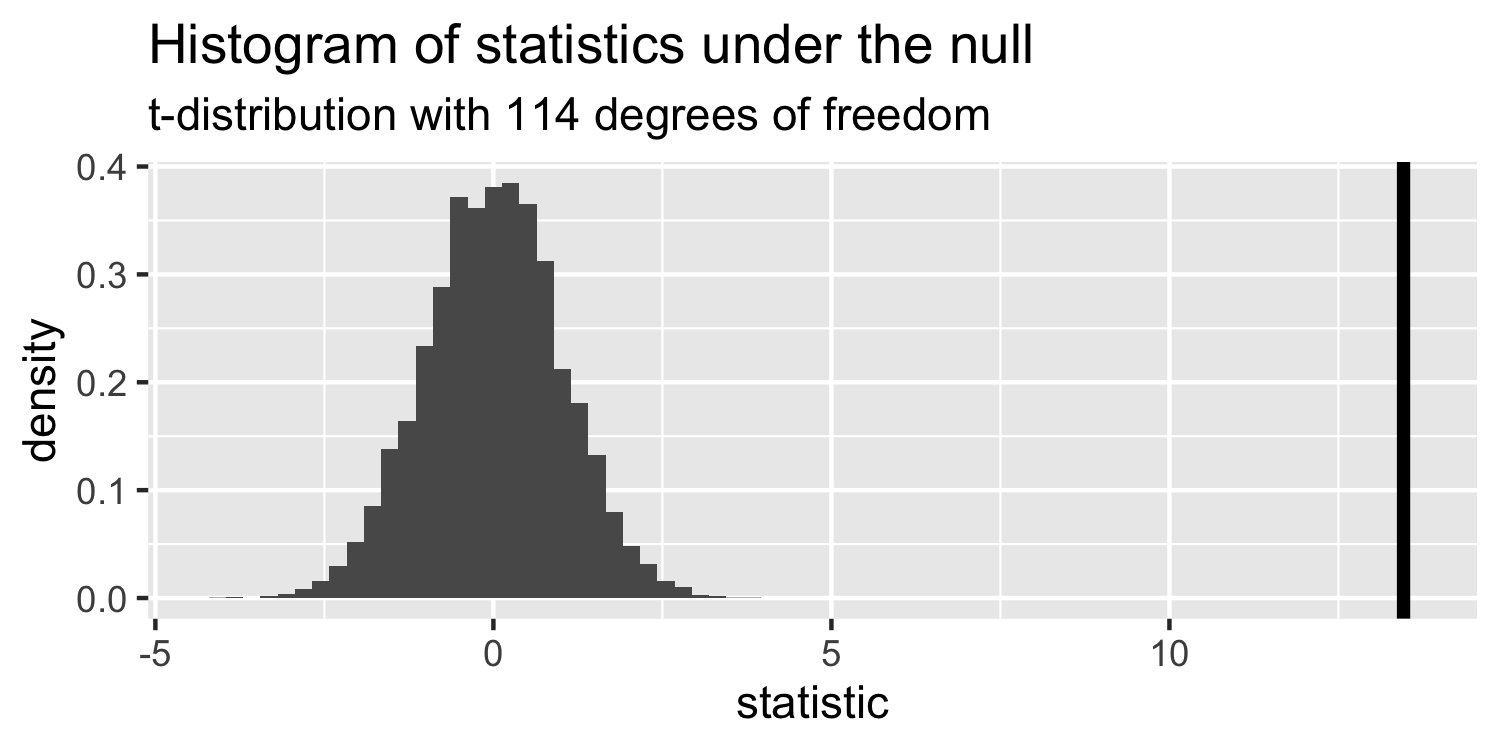
Sparrows
How can we compare this line to the distribution under the null?
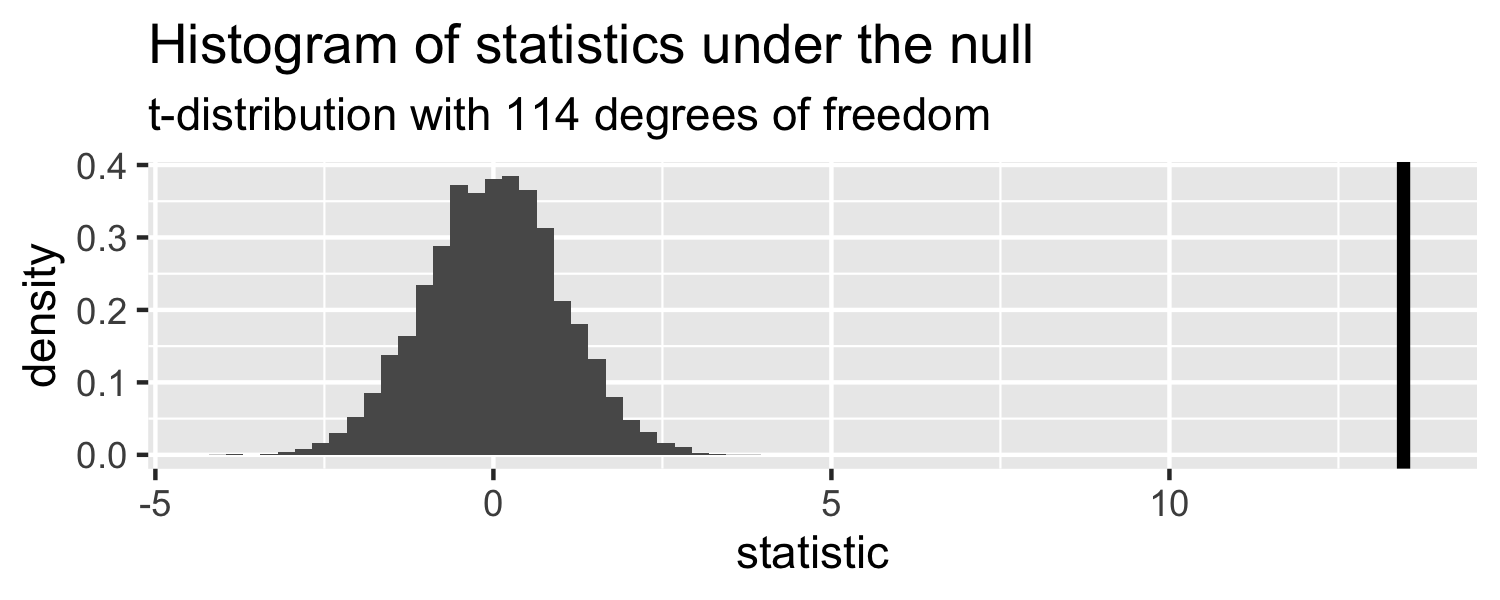
Sparrows
How can we compare this line to the distribution under the null?

- p-value
p-value
The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true
Sparrows
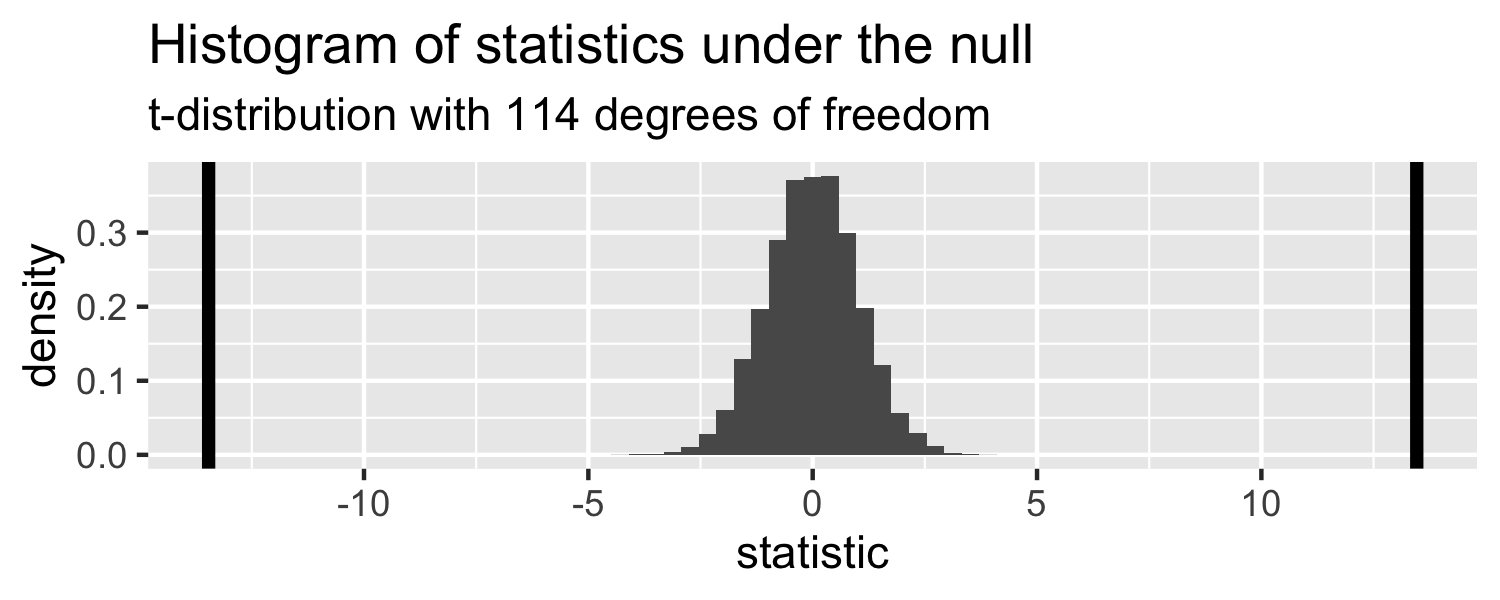
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Return to generated data, n = 20
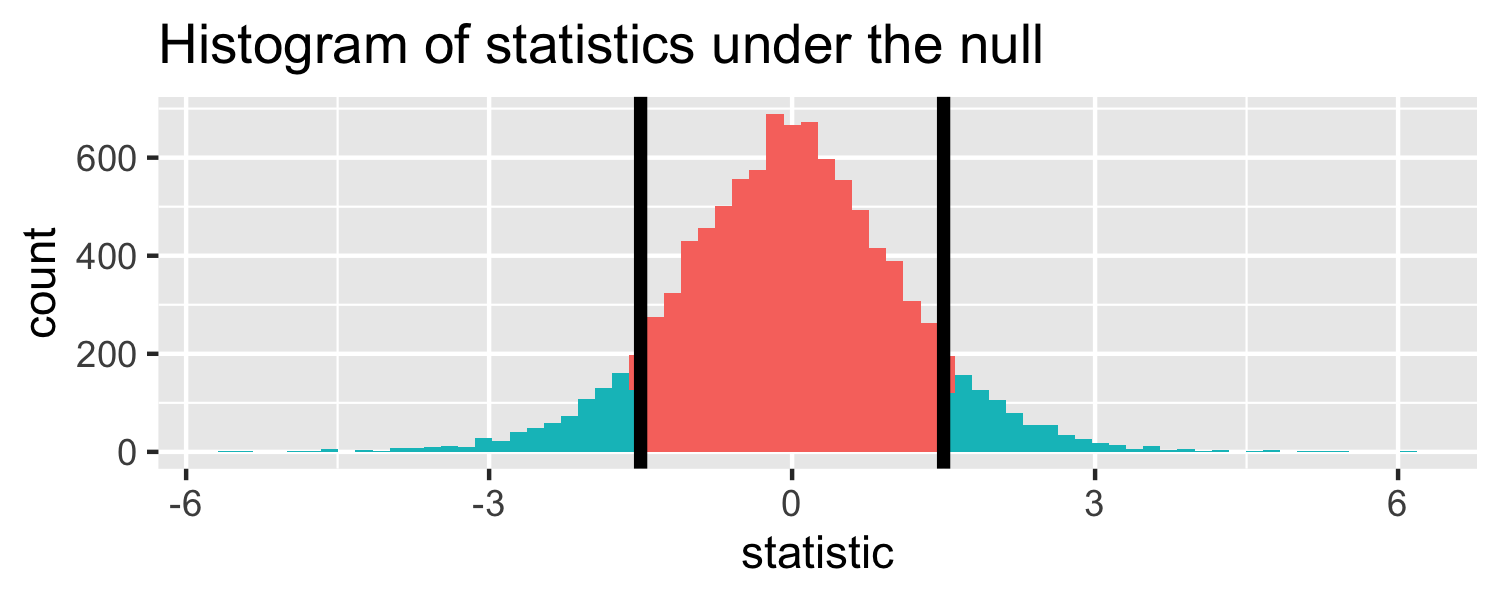
- Let's say we get a statistic of 1.5 in a sample
Let's do it in R!
The proportion of area less than 1.5
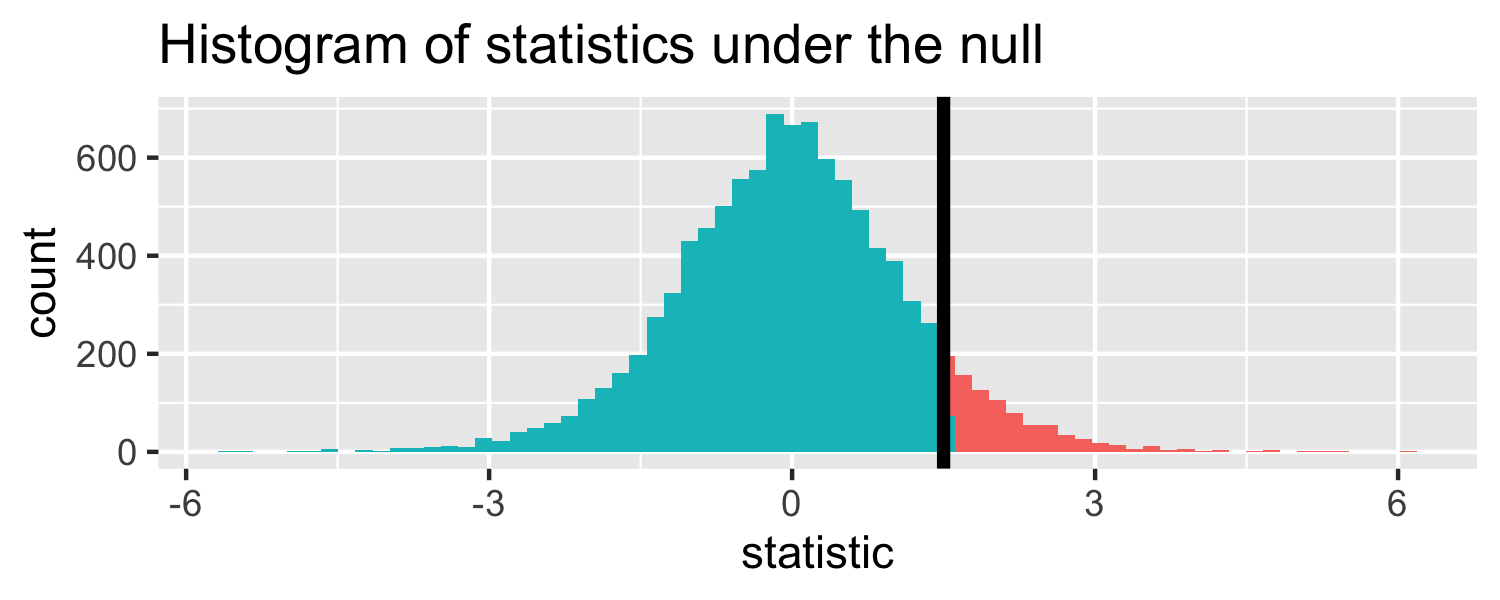
pt(1.5, df = 18)## [1] 0.9245248Let's do it in R!
The proportion of area greater than 1.5
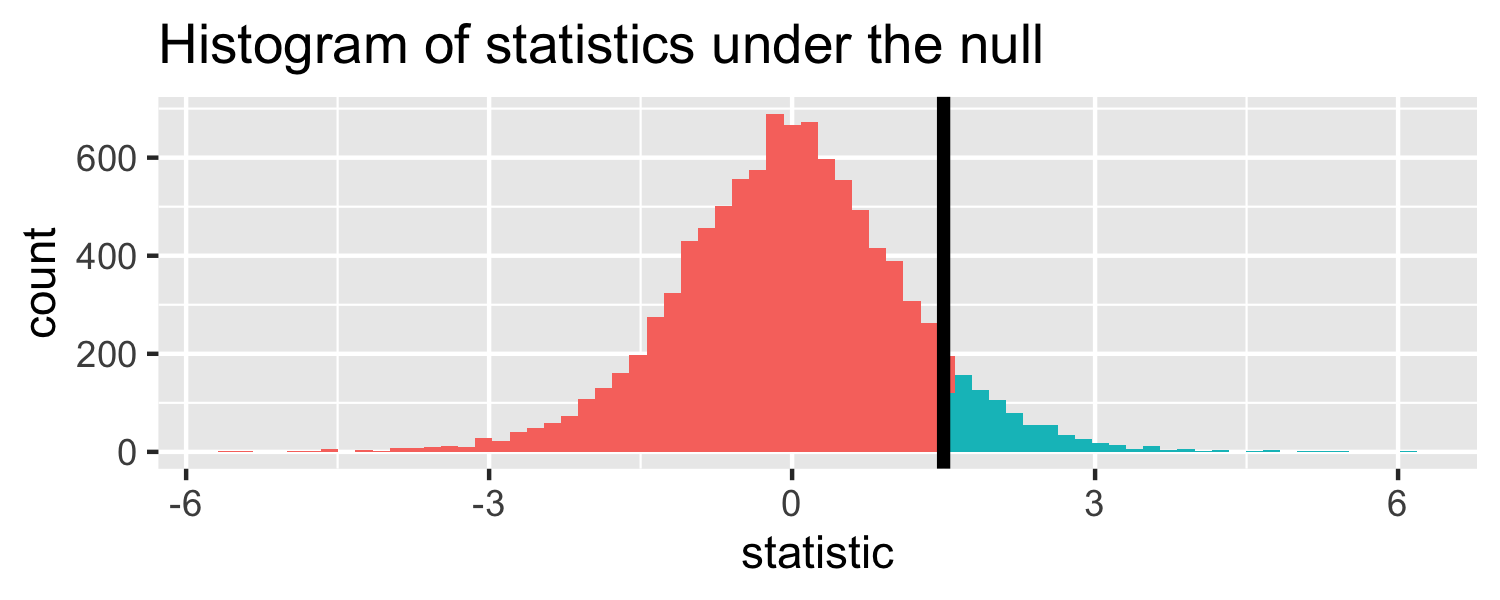
pt(1.5, df = 18, lower.tail = FALSE)## [1] 0.07547523Let's do it in R!
The proportion of area greater than 1.5 or less than -1.5.
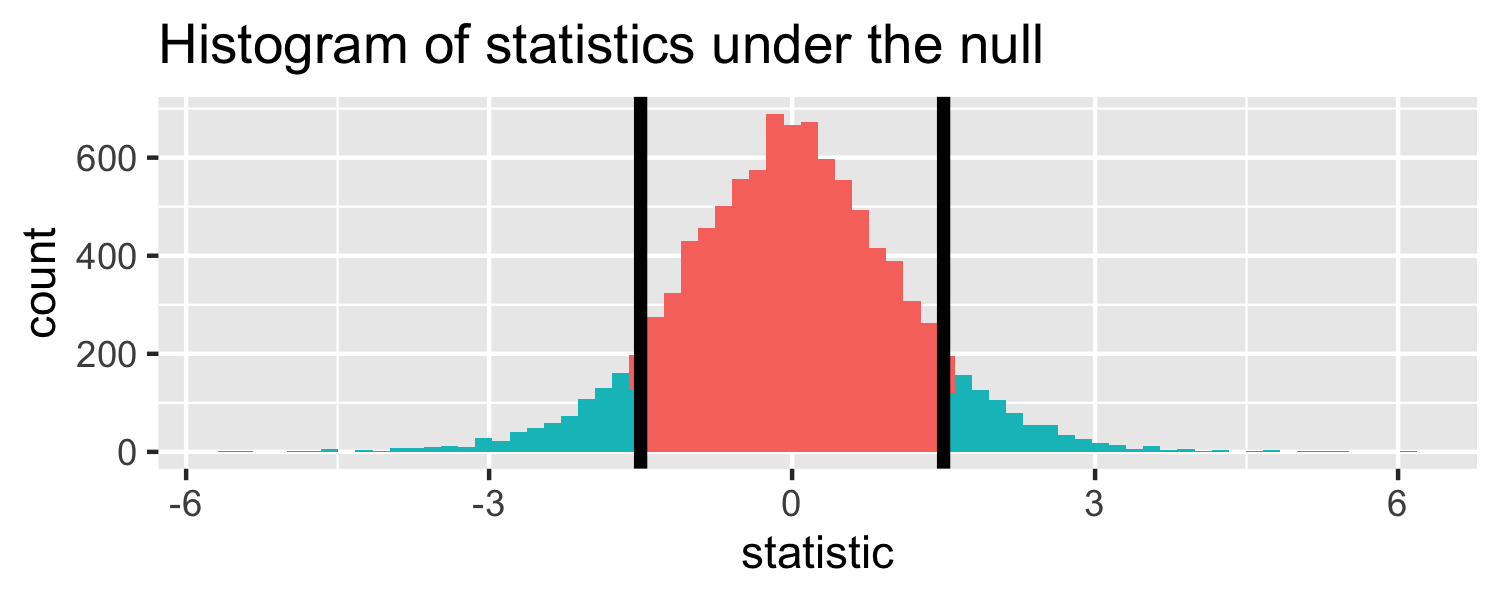
Let's do it in R!
The proportion of area greater than 1.5 or less than -1.5.

pt(1.5, df = 18, lower.tail = FALSE) * 2## [1] 0.1509505p-value
The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0 *p-value: 0.15
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0 p-value: 0.15 Often, we have an α-level cutoff to compare this to, for example 0.05. Since this is greater than 0.05, we fail to reject the null hypothesis
confidence intervals
If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( β1 ) to fall within the interval estimates 95% of the time.
Confidence interval
^β1±t∗×SE^β1
Confidence interval
(\Huge \hat\beta1 \pm t^∗ \times SE{\hat\beta_1})
- t∗ is the critical value for the tn−p−1 density curve to obtain the desired confidence level
Confidence interval
(\Huge \hat\beta1 \pm t^∗ \times SE{\hat\beta_1})
- t∗ is the critical value for the tn−p−1 density curve to obtain the desired confidence level Often we want a *95% confidence level.
Let's do it in R!
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536- t∗=tn−p−1=t114=1.98
Let's do it in R!
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536- t∗=tn−p−1=t114=1.98* LB=0.47−1.98×0.0347=0.399
- UB=0.47+1.98×0.0347=0.536
confidence intervals
If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( β1 ) to fall within the interval estimates 95% of the time.
Linear Regression Questions
- ✔️ Is there a relationship between a response variable and predictors?
- ✔️ How strong is the relationship?
- ✔️ What is the uncertainty?
- How accurately can we predict a future outcome?
Sparrows
Using the information here, how could I predict a new sparrow's weight if I knew the wing length was 30?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
Using the information here, how could I predict a new sparrow's weight if I knew the wing length was 30?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25- 1.37+0.467×30=15.38
Linear Regression Accuracy
What is the residual sum of squares again?
- Note: In previous classes, this may have been referred to as SSE (sum of squares error), the book uses RSS, so we will stick with that!
Linear Regression Accuracy
What is the residual sum of squares again?
- Note: In previous classes, this may have been referred to as SSE (sum of squares error), the book uses RSS, so we will stick with that!
RSS=∑(yi−^yi)2
Linear Regression Accuracy
What is the residual sum of squares again?
- Note: In previous classes, this may have been referred to as SSE (sum of squares error), the book uses RSS, so we will stick with that!
RSS=∑(yi−^yi)2
- The total sum of squares represents the variability of the outcome, it is equivalent to the variability described by the model plus the remaining residual sum of squares
TSS=∑(yi−¯y)2
Linear Regression Accuracy
- There are many ways "model fit" can be assessed. Two commone ones are:
- Residual Standard Error (RSE)
- R2 - the fraction of the variance explained
Linear Regression Accuracy
- There are many ways "model fit" can be assessed. Two commone ones are:
- Residual Standard Error (RSE)
- R2 - the fraction of the variance explained* RSE=√1n−p−1RSS
Linear Regression Accuracy
- There are many ways "model fit" can be assessed. Two commone ones are:
- Residual Standard Error (RSE)
- R2 - the fraction of the variance explained RSE=√1n−p−1RSS R2=1−RSSTSS
Linear Regression Accuracy
What could we use to determine whether at least one predictor is useful?
Linear Regression Accuracy
What could we use to determine whether at least one predictor is useful?
F=(TSS−RSS)/pRSS/(n−p−1)∼Fp,n−p−1 We can use a F-statistic!
Let's do it in R!
lm(Weight ~ WingLength, data = Sparrows) %>% glance()## # A tibble: 1 x 11## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419.## # … with 2 more variables: deviance <dbl>, df.residual <int>Additional Linear Regression Topics
- Polynomial terms
- Interactions
- Outliers
- Non-constant variance of error terms
- High leverage points
- Collinearity
Refer to Chapter 3 for more details on these topics if you need a refresher.
Linear Models
- Go back to your
Linear ModelsRStudio Cloud session - load the tidyverse and broom using
library(tidyverse)thenlibrary(broom) - Using the mtcars dataset, fit a model predicting
mpgfromam - Use the
tidy()function to see the beta coefficients - Use the
glance()function to see the model fit statistics - Knit, Commit, Push