Logistic regression, LDA, QDA
Dr. D’Agostino McGowan
☝️ Reminders
- Homework 1 is due tomorrow (be sure to knit, commit, push)
- Study sessions are 7-9 in Manchester 122
- Questions? Use github.com/sta-363-s20/community
📖 Canvas
- use Google Chrome
Recap
- Last class we had a linear regression refresher
Recap
- Last class we had a linear regression refresher
- We covered how to write a linear model in matrix form
Recap
- Last class we had a linear regression refresher
- We covered how to write a linear model in matrix form
- We learned how to minimize RSS to calculate ^β with (XTX)−1XTy
Recap
- Last class we had a linear regression refresher
- We covered how to write a linear model in matrix form
- We learned how to minimize RSS to calculate ^β with (XTX)−1XTy
- Linear regression is a great tool when we have a continuous outcome
- We are going to learn some fancy ways to do even better in the future
Classification
Classification
What are some examples of classification problems?
- Qualitative response variable in an unordered set, C
Classification
What are some examples of classification problems?
- Qualitative response variable in an unordered set, C
eye color∈{blue, brown, green}email∈{spam, not spam}
Classification
What are some examples of classification problems?
- Qualitative response variable in an unordered set, C
eye color∈{blue, brown, green}email∈{spam, not spam}
- Response, Y takes on values in C
- Predictors are a vector, X
Classification
What are some examples of classification problems?
- Qualitative response variable in an unordered set, C
eye color∈{blue, brown, green}email∈{spam, not spam}
- Response, Y takes on values in C
- Predictors are a vector, X
- The task: build a function C(X) that takes X and predicts Y, C(X)∈C
Classification
What are some examples of classification problems?
- Qualitative response variable in an unordered set, C
eye color∈{blue, brown, green}email∈{spam, not spam}
- Response, Y takes on values in C
- Predictors are a vector, X
- The task: build a function C(X) that takes X and predicts Y, C(X)∈C
- Many times we are actually more interested in the probabilities that X belongs to each category in C
Example: Credit card default
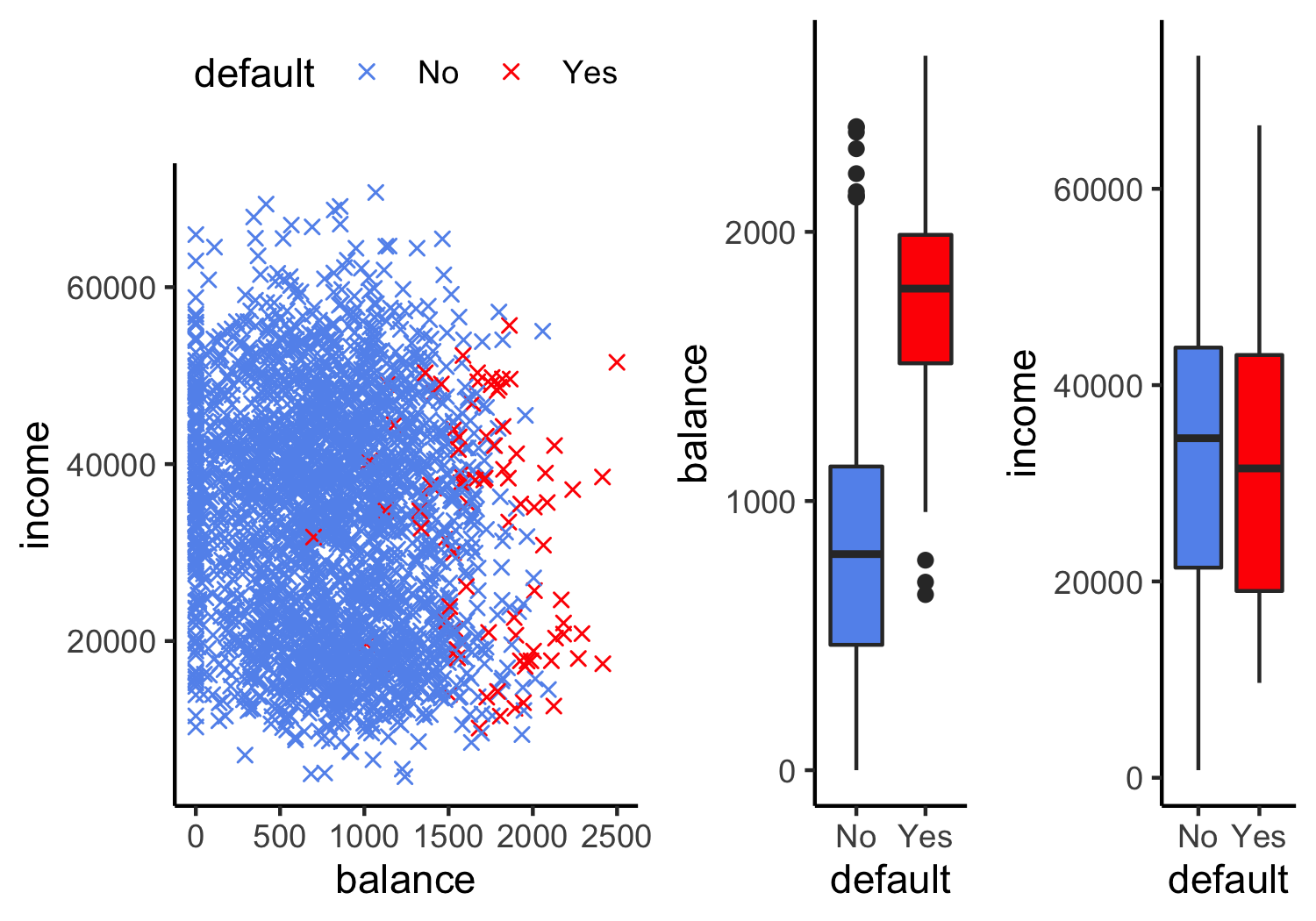
Can we use linear regression?
We can code Default as
Y={0if No1if Yes
Can we fit a linear regression of Y on X and classify as Yes if ^Y>0.5?
Can we use linear regression?
We can code Default as
Y={0if No1if Yes
Can we fit a linear regression of Y on X and classify as Yes if ^Y>0.5?
- In this case of a binary outcome, linear regression is okay (it is equivalent to linear discriminant analysis, we'll get to that soon!)
- E[Y|X=x]=P(Y=1|X=x), so it seems like this is a pretty good idea!
- The problem: Linear regression can produce probabilities less than 0 or greater than 1 😱
Can we use linear regression?
We can code Default as
Y={0if No1if Yes
Can we fit a linear regression of Y on X and classify as Yes if ^Y>0.5?
- In this case of a binary outcome, linear regression is okay (it is equivalent to linear discriminant analysis, we'll get to that soon!)
- E[Y|X=x]=P(Y=1|X=x), so it seems like this is a pretty good idea!
- The problem: Linear regression can produce probabilities less than 0 or greater than 1 😱
What may do a better job?
Can we use linear regression?
We can code Default as
Y={0if No1if Yes
Can we fit a linear regression of Y on X and classify as Yes if ^Y>0.5?
- In this case of a binary outcome, linear regression is okay (it is equivalent to linear discriminant analysis, we'll get to that soon!)
- E[Y|X=x]=P(Y=1|X=x), so it seems like this is a pretty good idea!
- The problem: Linear regression can produce probabilities less than 0 or greater than 1 😱
What may do a better job?
- Logistic regression!
Linear versus logistic regression
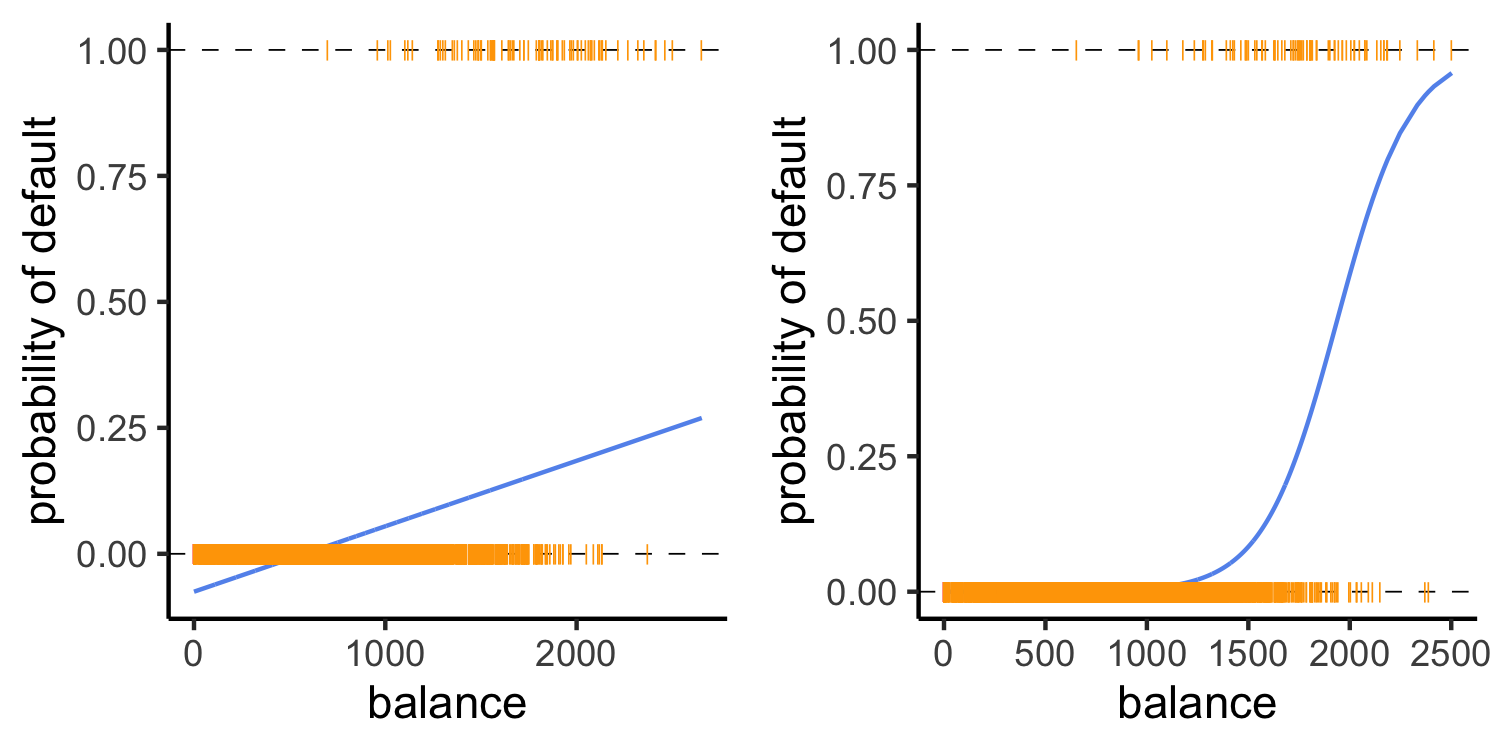
Which does a better job at predicting the probability of default?
- The orange marks represent the response Y∈{0,1}
Linear Regression
What if we have >2 possible outcomes? For example, someone comes to the emergency room and we need to classify them according to their symptoms
Y=⎧⎨⎩1if stroke2if drug overdose3if epileptic seizure
What could go wrong here?
Linear Regression
What if we have >2 possible outcomes? For example, someone comes to the emergency room and we need to classify them according to their symptoms
Y=⎧⎨⎩1if stroke2if drug overdose3if epileptic seizure
What could go wrong here?
- The coding implies an ordering
- The coding implies equal spacing (that is the difference between
strokeanddrug overdoseis the same asdrug overdoseandepileptic seizure)
Linear Regression
What if we have >2 possible outcomes? For example, someone comes to the emergency room and we need to classify them according to their symptoms
Y=⎧⎨⎩1if stroke2if drug overdose3if epileptic seizure
- Linear regression is not appropriate here
- Mutliclass logistic regression or discriminant analysis are more appropriate
Logistic Regression
p(X)=eβ0+β1X1+eβ0+β1X
- Note: p(X) is shorthand for P(Y=1|X)
- No matter what values β0, β1, or X take p(X) will always be between 0 and 1
Logistic Regression
p(X)=eβ0+β1X1+eβ0+β1X
- Note: p(X) is shorthand for P(Y=1|X)
- No matter what values β0, β1, or X take p(X) will always be between 0 and 1
- We can rearrange this into the following form: log(p(X)1−p(X))=β0+β1X
What is this transformation called?
Logistic Regression
p(X)=eβ0+β1X1+eβ0+β1X
- Note: p(X) is shorthand for P(Y=1|X)
- No matter what values β0, β1, or X take p(X) will always be between 0 and 1
- We can rearrange this into the following form: log(p(X)1−p(X))=β0+β1X
What is this transformation called?
- This is a log odds or logit transformation of p(X)
Linear versus logistic regression
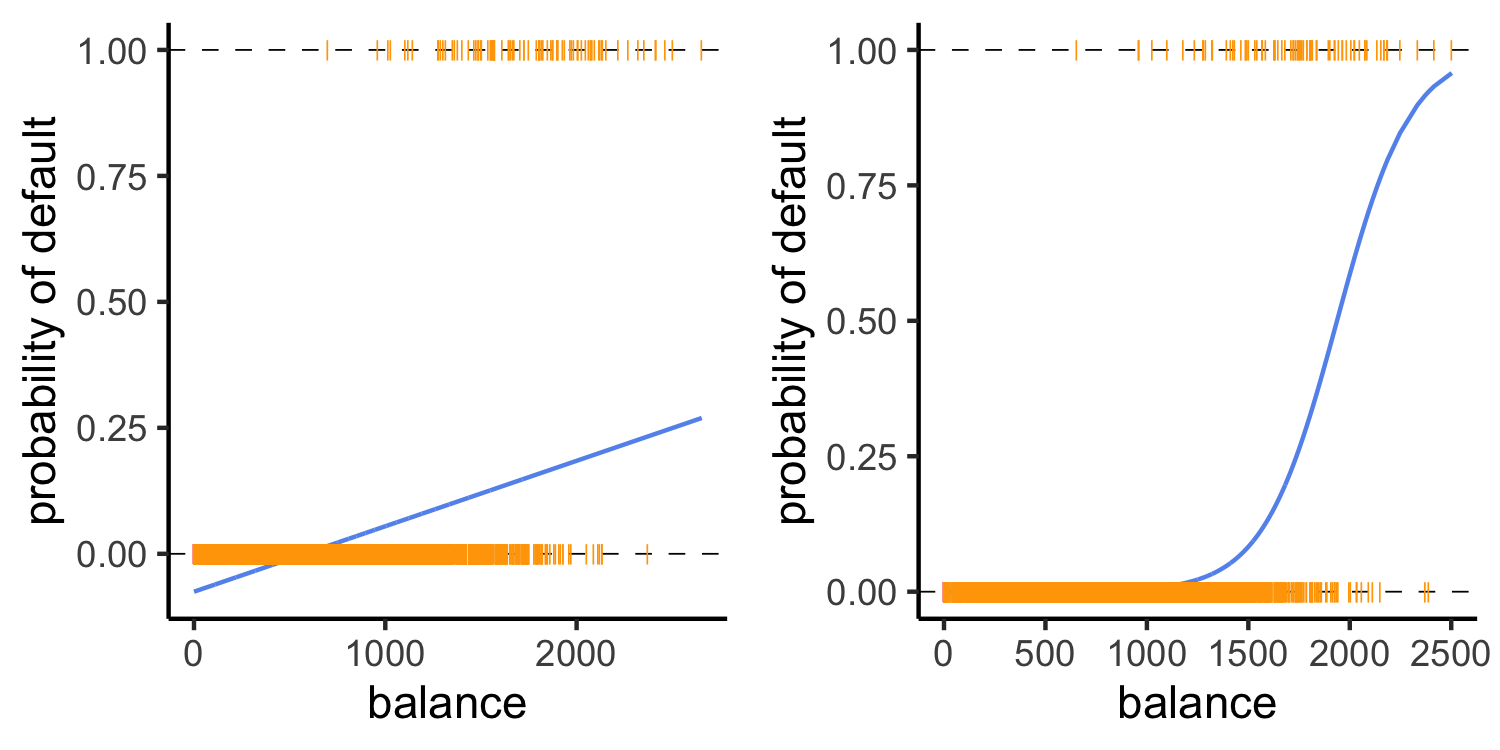
Logistic regression ensures that our estimates for p(X) are between 0 and 1 🎉
Maximum Likelihood
Refresher: How did we estimate ^β in linear regression?
Maximum Likelihood
Refresher: How did we estimate (\hat\beta) in linear regression?
l(β0,β1)=∏i:yi=1p(xi)∏i:yi=0(1−p(xi))
Maximum Likelihood
Refresher: How did we estimate (\hat\beta) in linear regression?
l(β0,β1)=∏i:yi=1p(xi)∏i:yi=0(1−p(xi))
- This likelihood give the probability of the observed ones and zeros in the data
- We pick β0 and β1 to maximize the likelihood
- We'll let
Rdo the heavy lifting here
Let's see it in R
glm(default ~ balance, data = Default, family = "binomial") %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -10.7 0.361 -29.5 3.62e-191## 2 balance 0.00550 0.000220 25.0 1.98e-137- Use the
glm()function in R with thefamily = "binomial"argument
Making predictions
What is our estimated probability of default for someone with a balance of $1000?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.6513306 | 0.3611574 | -29.49221 | 0 |
| balance | 0.0054989 | 0.0002204 | 24.95309 | 0 |
Making predictions
What is our estimated probability of default for someone with a balance of $1000?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.6513306 | 0.3611574 | -29.49221 | 0 |
| balance | 0.0054989 | 0.0002204 | 24.95309 | 0 |
^p(X)=e^β0+^β1X1+e^β0+^β1X=e−10.65+0.0055×10001+e−10.65+0.0055×1000=0.006
Making predictions
What is our estimated probability of default for someone with a balance of $2000?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.6513306 | 0.3611574 | -29.49221 | 0 |
| balance | 0.0054989 | 0.0002204 | 24.95309 | 0 |
Making predictions
What is our estimated probability of default for someone with a balance of $2000?
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.6513306 | 0.3611574 | -29.49221 | 0 |
| balance | 0.0054989 | 0.0002204 | 24.95309 | 0 |
^p(X)=e^β0+^β1X1+e^β0+^β1X=e−10.65+0.0055×20001+e−10.65+0.0055×2000=0.586
Logistic regression example
Let's refit the model to predict the probability of default given the customer is a student
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -3.5041278 | 0.0707130 | -49.554219 | 0.0000000 |
| studentYes | 0.4048871 | 0.1150188 | 3.520181 | 0.0004313 |
P(default = Yes|student = Yes)=e−3.5041+0.4049×11+e−3.5041+0.4049×1=0.0431
Logistic regression example
Let's refit the model to predict the probability of default given the customer is a student
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -3.5041278 | 0.0707130 | -49.554219 | 0.0000000 |
| studentYes | 0.4048871 | 0.1150188 | 3.520181 | 0.0004313 |
P(default = Yes|student = Yes)=e−3.5041+0.4049×11+e−3.5041+0.4049×1=0.0431
How will this change if student = No?
Logistic regression example
Let's refit the model to predict the probability of default given the customer is a student
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -3.5041278 | 0.0707130 | -49.554219 | 0.0000000 |
| studentYes | 0.4048871 | 0.1150188 | 3.520181 | 0.0004313 |
P(default = Yes|student = Yes)=e−3.5041+0.4049×11+e−3.5041+0.4049×1=0.0431
How will this change if student = No?
P(default = Yes|student = No)=e−3.5041+0.4049×01+e−3.5041+0.4049×0=0.0292
Multiple logistic regression
log(p(X)1−p(X))=β0+β1X1+⋯+βpXp p(X)=eβ0+β1X1+⋯+βpXp1+eβ0+β1X1+⋯+βpXp
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.8690452 | 0.4922555 | -22.080088 | 0.0000000 |
| balance | 0.0057365 | 0.0002319 | 24.737563 | 0.0000000 |
| income | 0.0000030 | 0.0000082 | 0.369815 | 0.7115203 |
| studentYes | -0.6467758 | 0.2362525 | -2.737646 | 0.0061881 |
Multiple logistic regression
log(p(X)1−p(X))=β0+β1X1+⋯+βpXp p(X)=eβ0+β1X1+⋯+βpXp1+eβ0+β1X1+⋯+βpXp
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -10.8690452 | 0.4922555 | -22.080088 | 0.0000000 |
| balance | 0.0057365 | 0.0002319 | 24.737563 | 0.0000000 |
| income | 0.0000030 | 0.0000082 | 0.369815 | 0.7115203 |
| studentYes | -0.6467758 | 0.2362525 | -2.737646 | 0.0061881 |
- Why is the coefficient for
studentnegative now when it was positive before?
Confounding
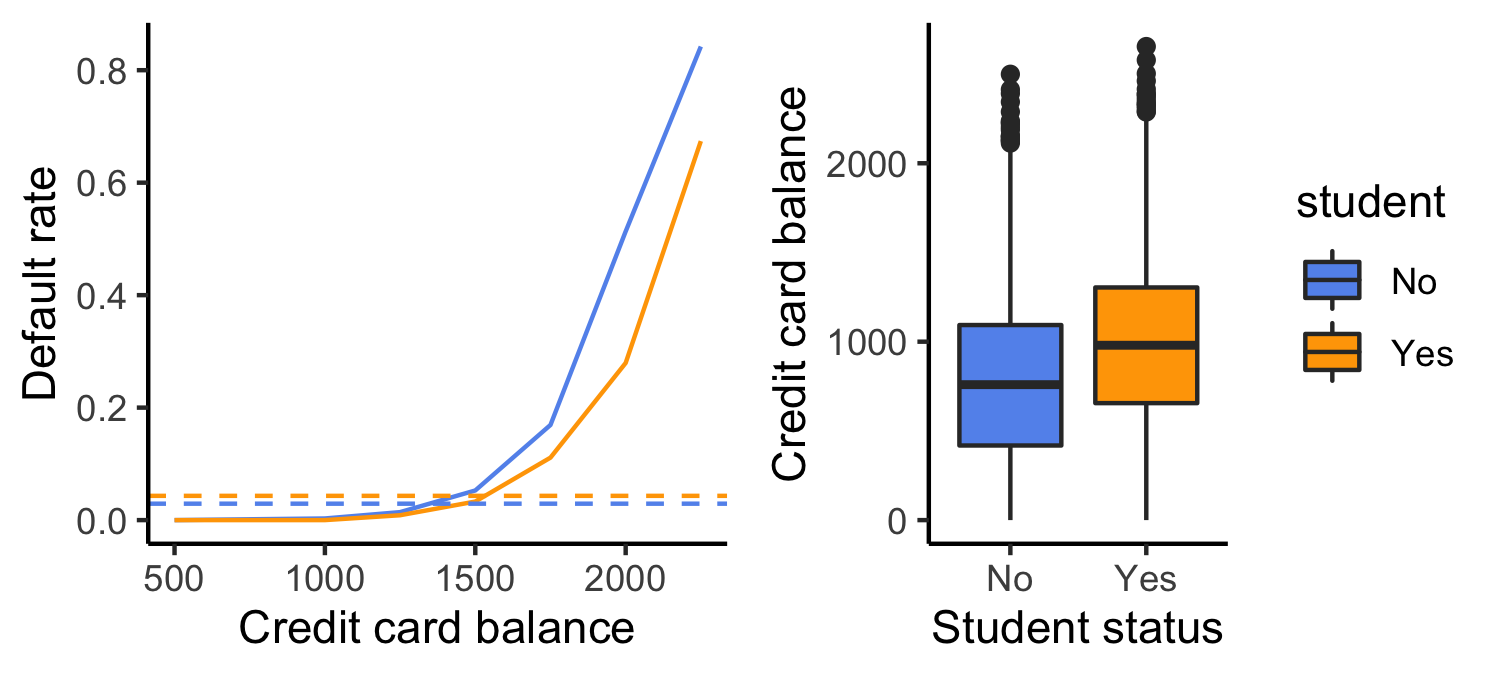
What is going on here?
Confounding
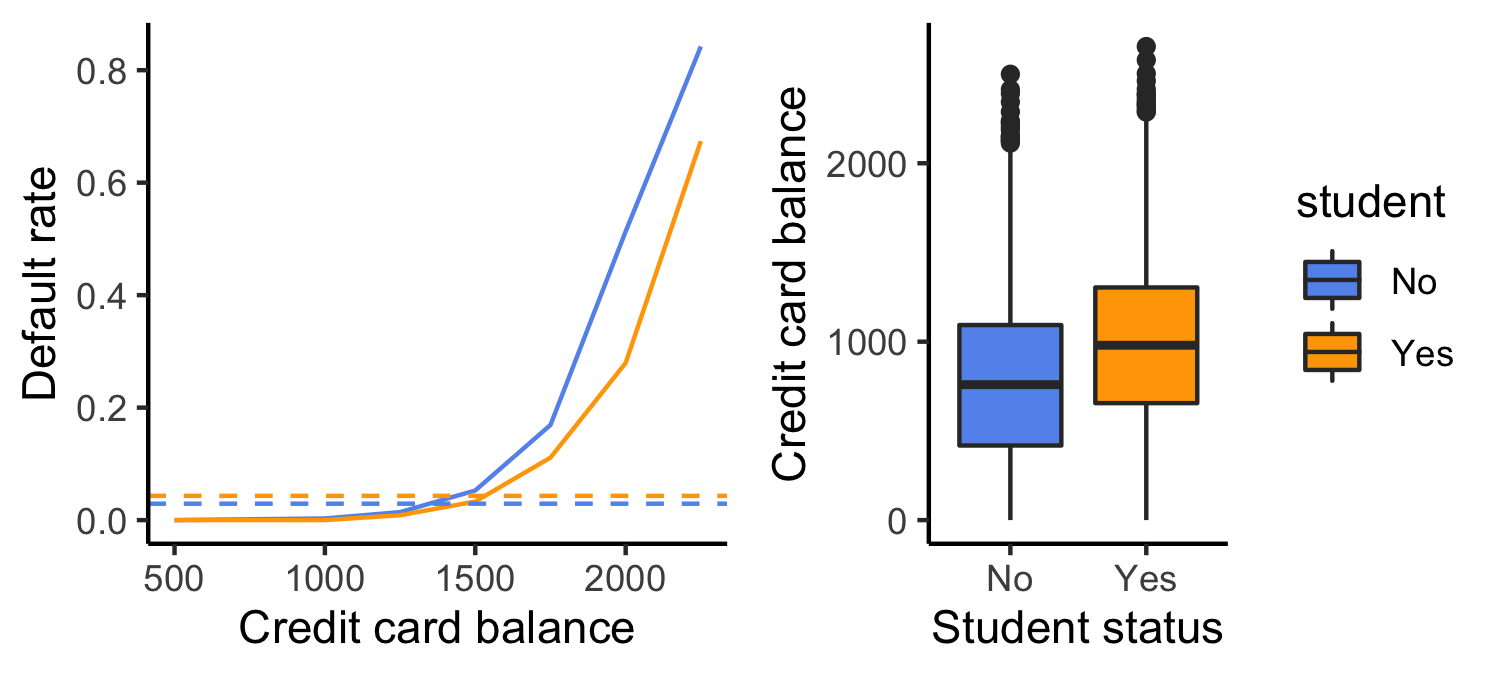
- Students tend to have higher balances than non-students
- Their marginal default rate is higher
Confounding

- Students tend to have higher balances than non-students
- Their marginal default rate is higher
- For each level of balance, students default less
- Their conditional default rate is lower
Logistic regression for more than two classes
- So far we've discussed binary outcome data
- We can generalize this to situations with multiple classes
P(Y=k|X)=eβ0k+β1kX1+⋯+βpkXp∑Kl=1eβ0l+β1lX1+⋯+βplXp
- Here we have a linear function for each of the K classes
- This is known as multinomial logistic regression
Discriminant Analysis
- Another way to model multiple classes 💡 Big idea:
- Model the distribution of X in each class separately ( P(X|Y) )
- Use Bayes theorem to flip things around to get P(Y|X)
Bayes Theorem
What is Bayes theorem?

Bayes Theorem
What is Bayes theorem?
P(Y=k|X=x)=P(X=x|Y=k)×P(Y=k)P(X=x)

Bayes Theorem
P(Y=k|X=x)=P(X=x|Y=k)×P(Y=k)P(X=x)
Bayes Theorem
P(Y=k|X=x)posterior=P(X=x|Y=k)×P(Y=k)P(X=x)
Bayes Theorem
P(Y=k|X=x)=likelihoodP(X=x|Y=k)×P(Y=k)P(X=x)
Bayes Theorem
P(Y=k|X=x)=likelihoodP(X=x|Y=k)×priorP(Y=k)P(X=x)
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)=P(+|Sick)P(Sick)P(+|Sick)P(Sick)+P(+|Healthy)P(Healthy)
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)=P(+|Sick)P(Sick)P(+|Sick)P(Sick)+P(+|Healthy)P(Healthy)
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)=P(+|Sick)P(Sick)P(+|Sick)P(Sick)+P(+|Healthy)P(Healthy)
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)=P(+|Sick)P(Sick)P(+|Sick)P(Sick)+P(+|Healthy)P(Healthy)
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
- Finally, let's suppose the disease is fairly common, 20% of people in the population have it.
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)=P(+|Sick)P(Sick)P(+|Sick)P(Sick)+P(+|Healthy)P(Healthy)
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
- Finally, let's suppose the disease is fairly common, 20% of people in the population have it.
What is my probability of having the disease given I tested positive?
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+).96=0.99×0.20.99×0.2+0.01×0.8
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
- Finally, let's suppose the disease is fairly common, 20% of people in the population have it.
What is my probability of having the disease given I tested positive?
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+).96=0.99×0.20.99×0.2+0.01×0.8
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
- If the disease is rare (let's say 0.1% have it) how does that change my probability of having it given a positive test?
What is my probability of having the disease given I tested positive?
Bayes Theorem Example
P(Sick|+)=P(+|Sick)P(Sick)P(+)0.09=0.99×0.0010.99×0.001+0.01×0.999
- Often when a test is created the sensitivity is calculated, that is the true positive rate, the P(+|Sick). Let's say in this case that is 99%
- Let's suppose the probability of a positive test if you are healthy is rare, 1%
- If the disease is rare (let's say 0.1% have it) how does that change my probability of having it given a positive test?
What is my probability of having the disease given I tested positive?
Bayes Theorem and Discriminant Analysis
P(Y|X)=P(X|Y)×P(Y)P(X)
This same equation is used for discriminant analysis with slightly different notation:
Bayes Theorem and Discriminant Analysis
P(Y|X)=P(X|Y)×P(Y)P(X)
This same equation is used for discriminant analysis with slightly different notation: P(Y|X)=πkfk(x)∑Kl=1fl(x)
Bayes Theorem and Discriminant Analysis
P(Y|X)=P(X|Y)×P(Y)P(X)
This same equation is used for discriminant analysis with slightly different notation: P(Y|X)=πkfk(x)∑Kl=1fl(x)
- fk(x)=P(X|Y) is the density for X in class k
- For linear discriminant analysis we will use the normal distribution to represent this density
Bayes Theorem and Discriminant Analysis
P(Y|X)=P(X|Y)×P(Y)P(X)
This same equation is used for discriminant analysis with slightly different notation: P(Y|X)=πkfk(x)∑Kl=1fl(x)
- fk(x)=P(X|Y) is the density for X in class k
- For linear discriminant analysis we will use the normal distribution to represent this density
- πk=P(Y) is the marginal or prior probability for class k
Discriminant analysis
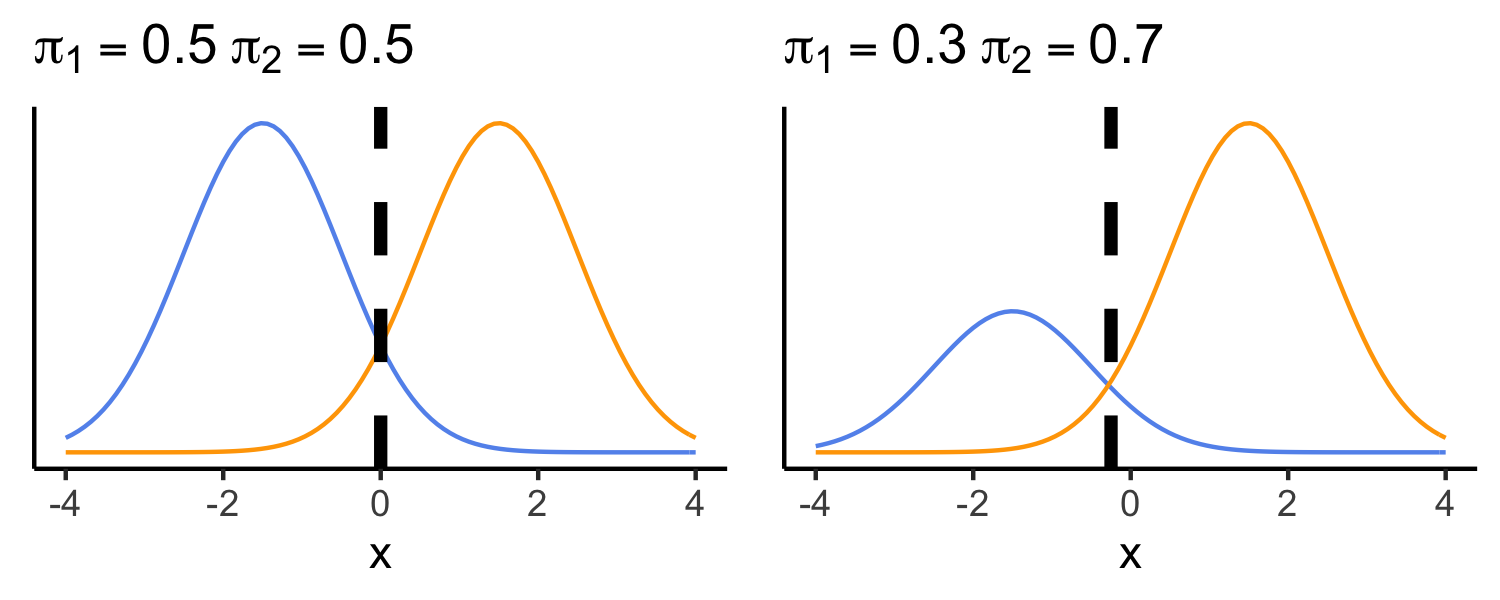
Discriminant analysis

- Here there are two classes
Discriminant analysis

- Here there are two classes
- We classify new points based on which density is highest
Discriminant analysis

- Here there are two classes
- We classify new points based on which density is highest
- On the left, the priors for the two classes are the same
Discriminant analysis

- Here there are two classes
- We classify new points based on which density is highest
- On the left, the priors for the two classes are the same
- On the right, we favor the orange class, making the decision boundary shift to the left
Why discriminant analysis?
- When the classes are well separated, logistic regression is unstable, linear discriminant analysis (LDA) is not
Why discriminant analysis?
- When the classes are well separated, logistic regression is unstable, linear discriminant analysis (LDA) is not
- When n is small and the distribution of predictors ( X ) is approximately normal in each class, the linear discriminant model is more stable than the logistic model
Why discriminant analysis?
- When the classes are well separated, logistic regression is unstable, linear discriminant analysis (LDA) is not
- When n is small and the distribution of predictors ( X ) is approximately normal in each class, the linear discriminant model is more stable than the logistic model
- When we have more than 2 classes, LDA also provides a nice low dimensional way to visualize data
Linear Discriminant Analysis p = 1
The density for the normal distribution is
fk(x)=1√2πσke−12(x−μkσk)2
Linear Discriminant Analysis p = 1
The density for the normal distribution is
fk(x)=1√2πσke−12(x−μkσk)2
- μk is the mean in class k
Linear Discriminant Analysis p = 1
The density for the normal distribution is
fk(x)=1√2πσke−12(x−μkσk)2
- μk is the mean in class k
- σ2k is the variance k (We will assume σk=σ are the same for all classes)
Linear Discriminant Analysis p = 1
The density for the normal distribution is
fk(x)=1√2πσke−12(x−μkσk)2
- We can plug this into Bayes formula
pk(X)=πk1√2πσke−12(x−μkσk)2∑kl=1πl1√2πσle−12(x−μlσl)2
Linear Discriminant Analysis p = 1
The density for the normal distribution is
fk(x)=1√2πσke−12(x−μkσk)2
- We can plug this into Bayes formula
pk(X)=πk1√2πσke−12(x−μkσk)2∑kl=1πl1√2πσle−12(x−μlσl)2
😅 Luckily things cancel!
Discriminant functions
- To classify an observation where X=x we need to determine which of the pk(x) is the largest
- It turns out this is equivalent to assigning x to the class with the largest discriminant score
δk(x)=xμkσ2−μ2k2σ2+log(πk)
Discriminant functions
- To classify an observation where X=x we need to determine which of the pk(x) is the largest
- It turns out this is equivalent to assigning x to the class with the largest discriminant score
δk(x)=xμkσ2−μ2k2σ2+log(πk)
- This discriminant score , δk(x), is a function of pk(x) (we took some logs and discarded terms that don't include k)
- δk(x) is a linear function of x
Discriminant functions
- To classify an observation where X=x we need to determine which of the pk(x) is the largest
- It turns out this is equivalent to assigning x to the class with the largest discriminant score
δk(x)=xμkσ2−μ2k2σ2+log(πk)
- This discriminant score , δk(x), is a function of pk(x) (we took some logs and discarded terms that don't include k)
- δk(x) is a linear function of x
If K=2, how do you think we would calculate the decision boundary?
Discriminant functions
δ1(x)=δ2(x)
Discriminant functions
δ1(x)=δ2(x)
- Let's set π1=π2=0.5
Discriminant functions
δ1(x)=δ2(x)
- Let's set π1=π2=0.5
xμ1σ2−μ212σ2+log(0.5)=xμ2σ2−μ222σ2+log(0.5)xμ1σ2−xμ2σ2=−μ222σ2+log(0.5)+μ212σ2−log(0.5)x(μ1−μ2)=μ21−μ222x=μ21−μ22(μ1−μ2)2x=(μ1−μ2)(μ1+μ2)(μ1−μ2)2x=μ1+μ22