Cross validation
Dr. D’Agostino McGowan
CV
- Go to the sta-363-s20 GitHub organization and search for
appex-03-cv - Clone this repository into RStudio Cloud
Cross validation
💡 Big idea
- We have determined that it is sensible to use a test set to calculate metrics like prediction error
Cross validation
💡 Big idea
- We have determined that it is sensible to use a test set to calculate metrics like prediction error
Why?
Cross validation
💡 Big idea
- We have determined that it is sensible to use a test set to calculate metrics like prediction error
How have we done this so far?
Cross validation
💡 Big idea
- We have determined that it is sensible to use a test set to calculate metrics like prediction error
- What if we don't have a seperate data set to test our model on?
Cross validation
💡 Big idea
- We have determined that it is sensible to use a test set to calculate metrics like prediction error
- What if we don't have a seperate data set to test our model on?
- 🎉 We can use resampling methods to estimate the test-set prediction error
Training error versus test error
What is the difference? Which is typically larger?
Training error versus test error
What is the difference? Which is typically larger?
- The training error is calculated by using the same observations used to fit the statistical learning model
Training error versus test error
What is the difference? Which is typically larger?
- The training error is calculated by using the same observations used to fit the statistical learning model
- The test error is calculated by using a statistical learning method to predict the response of new observations
Training error versus test error
What is the difference? Which is typically larger?
- The training error is calculated by using the same observations used to fit the statistical learning model
- The test error is calculated by using a statistical learning method to predict the response of new observations
- The training error rate typically underestimates the true prediction error rate
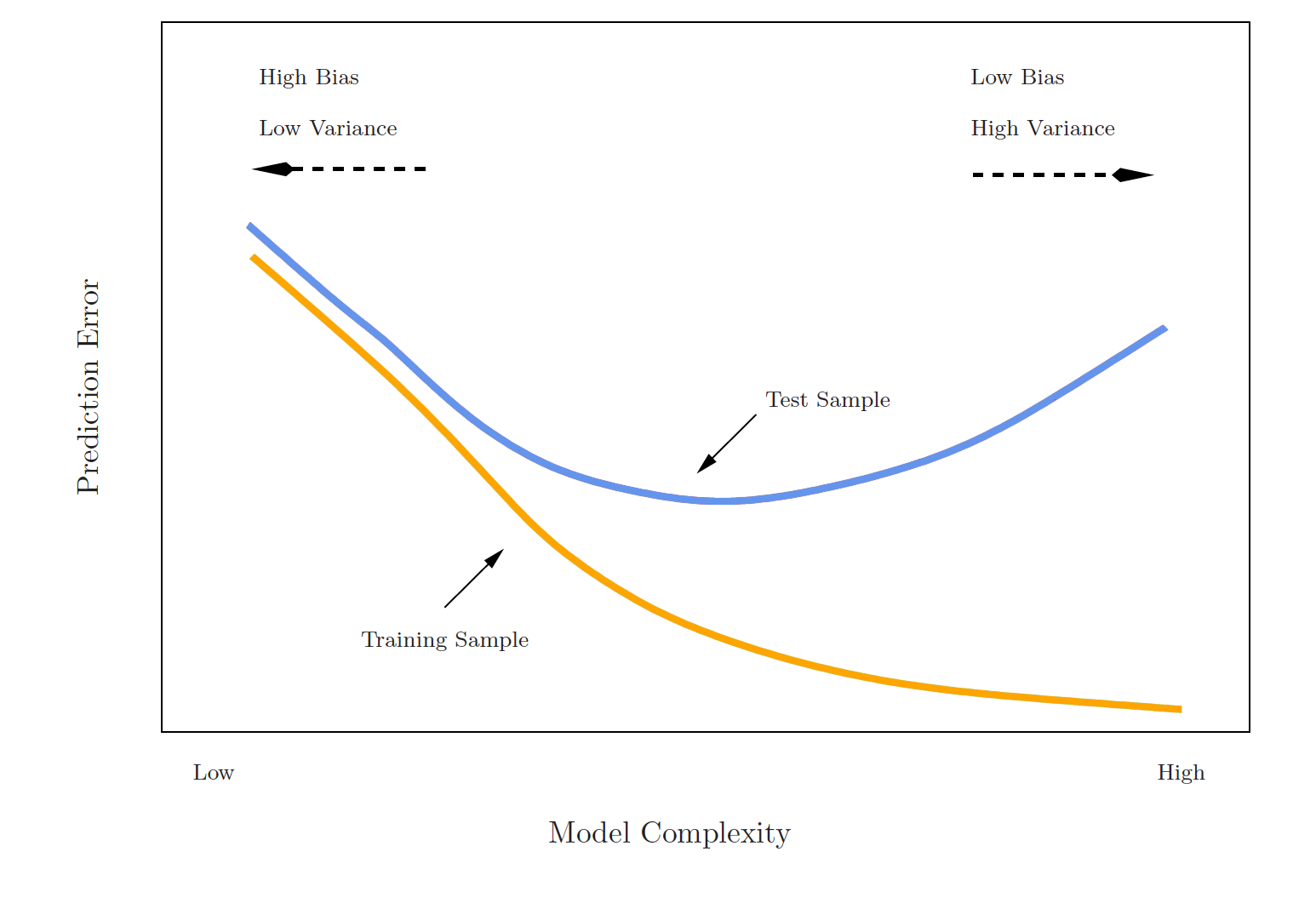
Estimating prediction error
- Best case scenario: We have a large data set to test our model on
Estimating prediction error
- Best case scenario: We have a large data set to test our model on
- This is not always the case!
Estimating prediction error
- Best case scenario: We have a large data set to test our model on
- This is not always the case!
💡 Let's instead find a way to estimate the test error by holding out a subset of the training observations from the model fitting process, and then applying the statistical learning method to those held out observations
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
- Fit the model on the training set, calculate the prediction error on the validation set
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
- Fit the model on the training set, calculate the prediction error on the validation set
If we have a quantitative predictor what metric would we use to calculate this test error?
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
- Fit the model on the training set, calculate the prediction error on the validation set
If we have a quantitative predictor what metric would we use to calculate this test error?
- Often we use Mean Squared Error (MSE)
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
- Fit the model on the training set, calculate the prediction error on the validation set
If we have a qualitative predictor (classification) what metric would we use to calculate this test error?
Approach #1: Validation set
- Randomly divide the available set up samples into two parts: a training set and a validation set
- Fit the model on the training set, calculate the prediction error on the validation set
If we have a qualitative predictor (classification) what metric would we use to calculate this test error?
- Often we use misclassification rate
Approach #1: Validation set
Auto example:
- We have 392 observations
- Trying to predict
mpgfromhorsepower - We can split the data in half and use 196 to fit the model and 196 to test
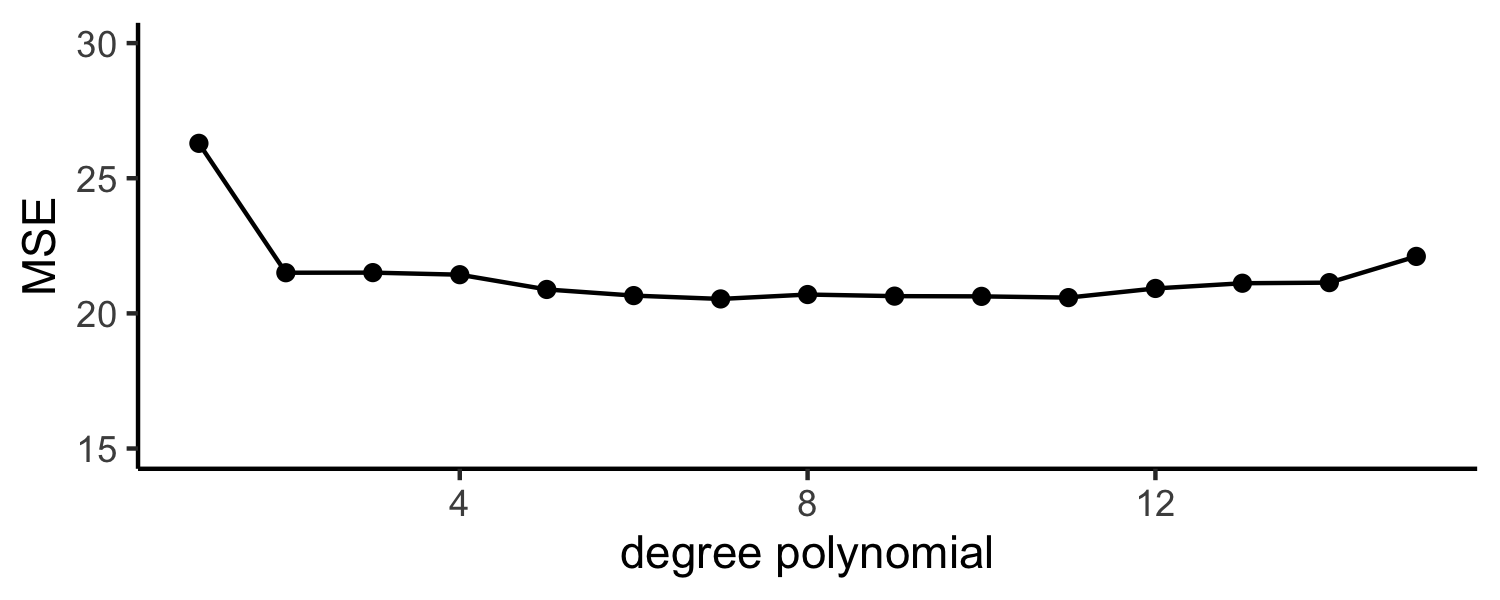
Approach #1: Validation set
Auto example:
- We have 392 observations
- Trying to predict
mpgfromhorsepower - We can split the data in half and use 196 to fit the model and 196 to test - what if we did this many times?
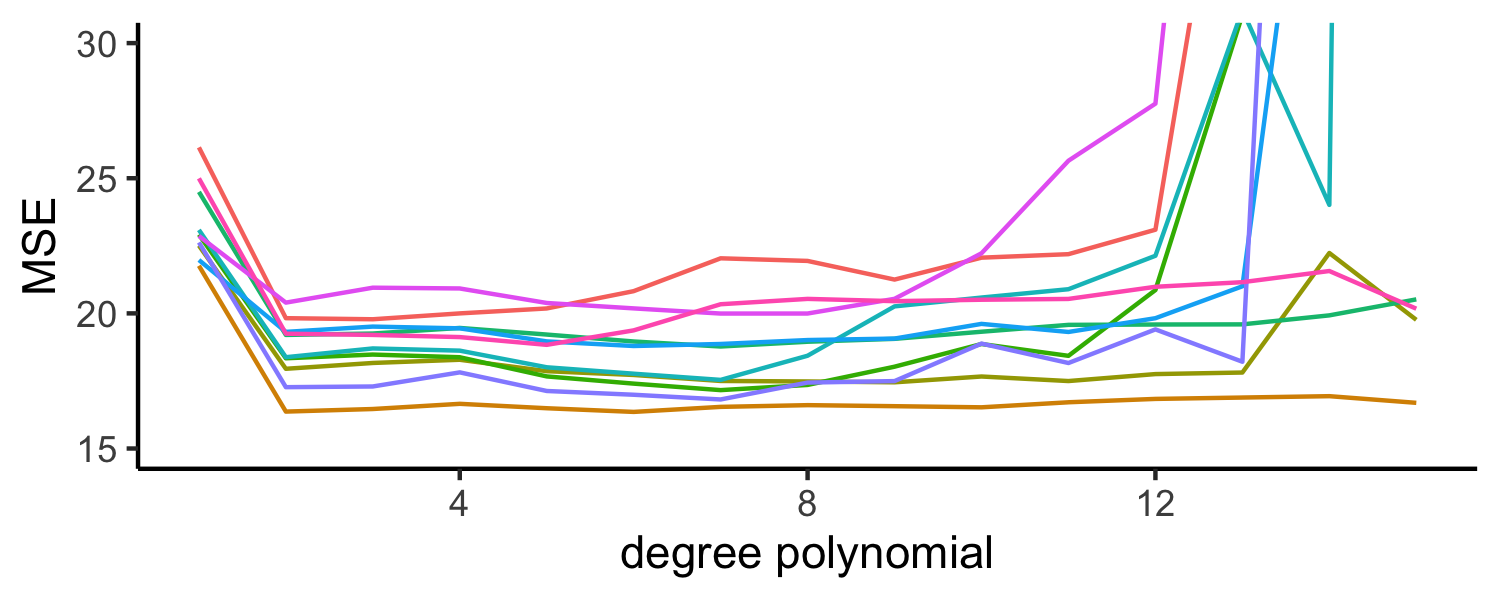
Approach #1: Validation set (Drawbacks)
- the validation estimate of the test error can be highly variable, depending on which observations are included in the training set and which observations are included in the validation set
Approach #1: Validation set (Drawbacks)
- the validation estimate of the test error can be highly variable, depending on which observations are included in the training set and which observations are included in the validation set
- In the validation approach, only a subset of the observations (those that are included in the training set rather than in the validation set) are used to fit the model
Approach #1: Validation set (Drawbacks)
- the validation estimate of the test error can be highly variable, depending on which observations are included in the training set and which observations are included in the validation set
- In the validation approach, only a subset of the observations (those that are included in the training set rather than in the validation set) are used to fit the model
- Therefore, the validation set error may tend to overestimate the test error for the model fit on the entire data set
Approach #2: K-fold cross validation
💡 The idea is to do the following:
- Randomly divide the data into \(K\) equal-sized parts
Approach #2: K-fold cross validation
💡 The idea is to do the following:
- Randomly divide the data into \(K\) equal-sized parts
- Leave out part \(k\), fit the model to the other \(K - 1\) parts (combined)
Approach #2: K-fold cross validation
💡 The idea is to do the following:
- Randomly divide the data into \(K\) equal-sized parts
- Leave out part \(k\), fit the model to the other \(K - 1\) parts (combined)
- Obtain predictions for the left-out \(k\)th part
Approach #2: K-fold cross validation
💡 The idea is to do the following:
- Randomly divide the data into \(K\) equal-sized parts
- Leave out part \(k\), fit the model to the other \(K - 1\) parts (combined)
- Obtain predictions for the left-out \(k\)th part
- Do this for each part \(k = 1, 2,\dots K\), and then combine the results
Let's do it in R!
sample(1:nrow(Auto))## [1] 266 72 207 312 122 268 299 101 261 380 211 355 79 88 183 174 295 1## [19] 281 310 118 265 94 115 257 156 313 196 200 307 137 60 69 308 121 277## [37] 25 86 381 362 363 340 304 153 67 29 202 356 182 162 17 203 270 204## [55] 10 134 36 9 374 109 98 273 353 4 18 239 24 23 390 337 139 26## [73] 89 254 347 379 44 209 359 348 117 37 242 21 373 39 238 111 188 278## [91] 32 216 47 383 231 177 318 300 324 386 87 164 385 288 62 170 389 154## [109] 230 329 191 248 369 250 225 15 263 138 330 55 186 149 165 83 316 227## [127] 48 367 368 141 213 287 201 335 145 31 176 234 143 146 131 166 148 20## [145] 352 244 247 73 193 167 332 96 262 197 64 43 226 327 82 235 3 50## [163] 382 12 199 271 298 232 328 172 8 223 292 221 222 80 45 208 358 370## [181] 171 35 387 245 240 22 124 309 365 372 284 105 11 311 7 255 140 354## [199] 93 74 150 184 85 53 123 142 110 68 215 27 49 302 343 290 61 51## [217] 132 99 175 272 251 256 130 321 289 349 269 5 246 351 303 276 243 187## [235] 136 249 346 107 100 14 91 319 157 293 275 65 59 54 219 16 282 113## [253] 325 70 192 95 66 296 97 301 322 78 377 6 81 294 90 34 338 317## [271] 92 205 169 342 38 252 258 120 129 241 52 163 228 334 280 339 264 181## [289] 194 267 364 77 42 127 375 180 345 214 135 190 220 133 151 119 320 210## [307] 198 185 392 128 391 58 206 13 378 179 212 41 19 104 331 147 46 2## [325] 195 306 253 30 297 103 279 33 102 260 274 71 152 161 126 236 360 388## [343] 155 106 341 160 114 75 224 178 305 376 384 63 350 357 366 116 217 40## [361] 218 108 233 336 371 112 229 84 314 168 323 237 28 326 315 56 286 76## [379] 285 125 57 344 283 259 173 159 158 333 361 144 189 291Let's do it in R!
What is this code doing?
sample(1:nrow(Auto))## [1] 146 341 313 69 64 366 172 31 379 7 190 163 145 280 106 248 294 271## [19] 368 203 246 103 147 207 361 355 80 144 318 252 122 250 56 320 319 50## [37] 13 127 135 218 179 119 116 201 18 140 91 59 21 19 333 375 11 185## [55] 6 262 255 4 274 286 141 210 138 107 363 231 300 199 343 238 292 226## [73] 339 181 117 177 284 86 260 212 281 93 120 384 241 167 189 283 92 111## [91] 291 367 170 240 143 259 208 38 192 235 71 328 139 96 287 353 354 74## [109] 109 85 217 121 184 68 83 258 39 133 220 304 149 14 359 142 104 345## [127] 391 90 347 95 314 356 324 176 42 150 24 168 346 60 327 8 110 243## [145] 99 228 25 79 129 348 206 102 323 115 216 5 46 254 72 124 169 221## [163] 239 385 290 321 22 202 76 378 40 78 276 365 52 195 285 325 329 362## [181] 157 236 65 358 41 317 196 57 386 30 153 265 376 301 33 81 193 29## [199] 173 295 310 152 264 298 377 118 305 47 340 387 332 256 178 392 175 383## [217] 100 322 183 70 188 45 272 336 390 165 374 357 306 166 174 308 303 214## [235] 382 108 156 334 299 3 155 307 101 112 51 277 232 293 273 229 244 278## [253] 209 263 16 73 269 344 245 364 158 62 337 261 242 32 219 279 128 372## [271] 326 335 234 249 389 54 58 61 44 105 49 28 97 20 10 26 126 88## [289] 233 316 134 171 48 98 9 352 131 130 123 373 197 237 247 148 312 2## [307] 17 282 132 330 315 349 198 187 227 350 159 137 270 289 204 222 55 351## [325] 34 180 215 67 87 94 84 380 161 211 154 12 288 338 213 160 369 253## [343] 309 296 23 182 360 331 225 27 162 75 302 82 53 370 230 205 136 200## [361] 113 223 267 191 186 43 194 311 66 164 114 381 388 89 275 125 77 35## [379] 297 251 371 15 1 257 266 36 37 342 224 268 63 151Let's do it in R!
K <- 5Auto <- Auto %>% slice(sample(1:nrow(Auto))) %>% mutate(k = rep(1:K, length.out = nrow(Auto)))Let's do it in R!
K <- 5Auto <- Auto %>% slice(sample(1:nrow(Auto))) %>% mutate(k = rep(1:K, length.out = nrow(Auto)))Let's do it in R!
K <- 5Auto <- Auto %>% slice(sample(1:nrow(Auto))) %>% mutate(k = rep(1:K, length.out = nrow(Auto)))Auto %>% group_by(k) %>% summarise(n = n())## # A tibble: 5 x 2## k n## <int> <int>## 1 1 79## 2 2 79## 3 3 78## 4 4 78## 5 5 78Estimating prediction error (quantitative outcome)
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k$$
Estimating prediction error (quantitative outcome)
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k$$
- \(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
Estimating prediction error (quantitative outcome)
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k$$
- \(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
- \(n_k\) is the number of observations in group \(k\)
- \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
Estimating prediction error (quantitative outcome)
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_{(K)} = \sum_{k=1}^K\frac{n_k}{n}MSE_k$$
- \(MSE_k = \sum_{i \in C_k} (y_i - \hat{y}_i)^2/n_k\)
- \(n_k\) is the number of observations in group \(k\)
- \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
- If we set \(K = n\), we'd have \(n-fold\) cross validation which is the same as leave-one-out cross validation (LOOCV)
Let's see it in R!
What pieces of the equation have a k in them?
Let's see it in R!
What pieces of the equation have a k in them?
Auto1 <- Auto %>% filter(k != 1)model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1)model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79- Now we just have to do this 4 more times!
Let's see it in R!
Auto1 <- Auto %>% filter(k != 1) model1 <- lm(mpg ~ horsepower, data = Auto1)Auto %>% filter(k == 1) %>% mutate(p = predict(model1, newdata = .)) %>% summarise(mse_1 = mean((mpg - p)^2), n_1 = n())## mse_1 n_1## 1 23.02586 79- Now we just have to do this 4 more times! 😅
👍 If you have to copy/paste code more than 3 times, write a function!
Let's see it in R!
mse_k <- function(K = 1) { Auto_k <- Auto %>% filter(k != K) model_k <- lm(mpg ~ horsepower, data = Auto_k) Auto %>% filter(k == K) %>% mutate(p = predict(model_k, newdata = .)) %>% summarise(mse_k = mean((mpg - p)^2), n_k = n())}Let's see it in R!
mse_k <- function(K = 1) { Auto_k <- Auto %>% filter(k != K) model_k <- lm(mpg ~ horsepower, data = Auto_k) Auto %>% filter(k == K) %>% mutate(p = predict(model_k, newdata = .)) %>% summarise(mse_k = mean((mpg - p)^2), n_k = n())}Let's see it in R!
mse_k()## mse_k n_k## 1 23.02586 79Let's see it in R!
mse_k(K = 1)## mse_k n_k## 1 23.02586 79Let's see it in R!
mse_k(K = 1)## mse_k n_k## 1 23.02586 79mse_k(K = 2)## mse_k n_k## 1 30.922 79mse_k(K = 3)## mse_k n_k## 1 19.48487 78Let's see it in R!
mse_k(K = 1)## mse_k n_k## 1 23.02586 79mse_k(K = 2)## mse_k n_k## 1 30.922 79mse_k(K = 3)## mse_k n_k## 1 19.48487 78- Uh-oh we are copy/pasting again!
purrr \(\in\) tidyverse

- purrr is a package for iterating in R
- The functions we will use are all
map_xxx()functions
map(.x, .f, ...)
map(.x, .f, ...)
for every element of .x do .f
Example
map(1:5, ~ .x * 2)## [[1]]## [1] 2## ## [[2]]## [1] 4## ## [[3]]## [1] 6## ## [[4]]## [1] 8## ## [[5]]## [1] 10Example
map(1:5, ~ .x * 2)## [[1]]## [1] 2## ## [[2]]## [1] 4## ## [[3]]## [1] 6## ## [[4]]## [1] 8## ## [[5]]## [1] 10- By default, the output will be a list
Example
map(1:5, ~ .x * 2)## [[1]]## [1] 2## ## [[2]]## [1] 4## ## [[3]]## [1] 6## ## [[4]]## [1] 8## ## [[5]]## [1] 10- By default, the output will be a list
- You can dictate your desired output type by specifying
map_xxx()for example to output a numeric (double) vector, usemap_dbl()
Example
map_dbl(1:5, ~ .x * 2)## [1] 2 4 6 8 10map_xxx(.x, .f)
map(): listmap_dbl(): doublemap_int()map_lgl()map_chr()map_df()
map_xxx(.x, .f)
map(): listmap_dbl(): doublemap_int()map_lgl()map_chr()map_df()
What do you think the rest of these output?
map_xxx(.x, .f)
map(): listmap_dbl(): doublemap_int(): integermap_lgl(): logicalmap_chr(): charactermap_df(): data frame
What do you think the rest of these output?
Back to our example!
map(1:K, ~ mse_k(.x))## [[1]]## mse_k n_k## 1 23.02586 79## ## [[2]]## mse_k n_k## 1 30.922 79## ## [[3]]## mse_k n_k## 1 19.48487 78## ## [[4]]## mse_k n_k## 1 19.9612 78## ## [[5]]## mse_k n_k## 1 26.69468 78How can I get these into a data frame?
Let's see it in R!
map_df(1:K, ~ mse_k(.x))## mse_k n_k## 1 23.02586 79## 2 30.92200 79## 3 19.48487 78## 4 19.96120 78## 5 26.69468 78Let's see it in R!
map_df(1:K, ~ mse_k(.x))## mse_k n_k## 1 23.02586 79## 2 30.92200 79## 3 19.48487 78## 4 19.96120 78## 5 26.69468 78What do I need to do with these to estimate the prediction error?
map_df(1:K, ~ mse_k(.x)) %>% summarise(cv_5 = sum(n_k / sum(n_k) * mse_k))## cv_5## 1 24.03281Special Case!
- With linear regression, you can actually calculate the LOOCV error without having to iterate!
$$CV_{(n)} = \frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2$$
Special Case!
- With linear regression, you can actually calculate the LOOCV error without having to iterate!
$$CV_{(n)} = \frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2$$
- \(\hat{y}_i\) is the \(i\)th fitted value from the linear model
Special Case!
- With linear regression, you can actually calculate the LOOCV error without having to iterate!
$$CV_{(n)} = \frac{1}{n}\sum_{i=1}^n\left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2$$
- \(\hat{y}_i\) is the \(i\)th fitted value from the linear model
- \(h_i\) is the diagonal of the "hat" matrix (remember that! 🎓)
Picking \(K\)
- \(K\) can vary from 2 (splitting the data in half each time) to \(n\) (LOOCV)
Picking \(K\)
- \(K\) can vary from 2 (splitting the data in half each time) to \(n\) (LOOCV)
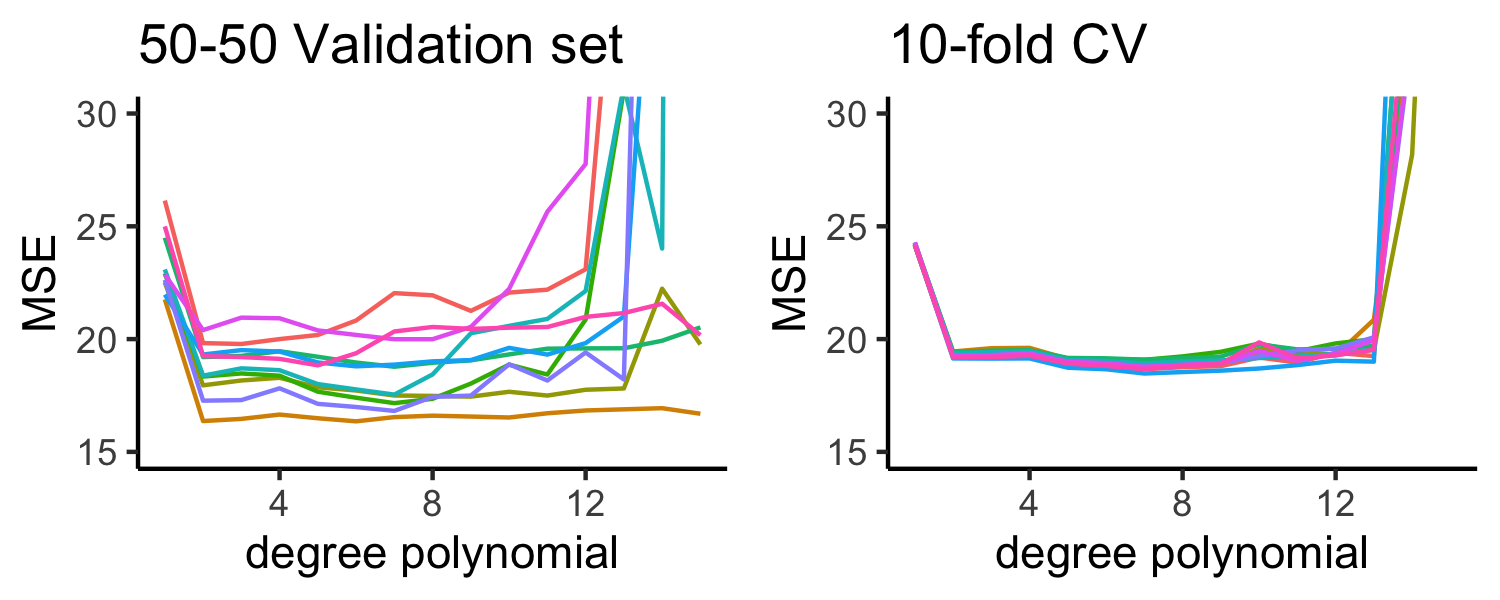
- LOOCV is sometimes useful but usually the estimates from each fold are very correlated, so their average can have a high variance
Picking \(K\)
- \(K\) can vary from 2 (splitting the data in half each time) to \(n\) (LOOCV)
- LOOCV is sometimes useful but usually the estimates from each fold are very correlated, so their average can have a high variance
- A better choice tends to be \(K=5\) or \(K=10\)
Bias variance trade-off
- Since each training set is only \((K - 1)/K\) as big as the original training set, the estimates of prediction error will typically be biased upward
Bias variance trade-off
- Since each training set is only \((K - 1)/K\) as big as the original training set, the estimates of prediction error will typically be biased upward
- This bias is minimized when \(K = n\) (LOOCV), but this estimate has a high variance
Bias variance trade-off
- Since each training set is only \((K - 1)/K\) as big as the original training set, the estimates of prediction error will typically be biased upward
- This bias is minimized when \(K = n\) (LOOCV), but this estimate has a high variance
- \(K =5\) or \(K=10\) provides a nice compromise for the bias-variance trade-off
Approach #2: K-fold Cross Validation
Auto example:
- We have 392 observations
- Trying to predict
mpgfromhorsepower
Estimating prediction error (qualitative outcome)
- The premise is the same as cross valiation for quantitative outcomes
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k$$
Estimating prediction error (qualitative outcome)
- The premise is the same as cross valiation for quantitative outcomes
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k$$
- \(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (missclassification rate)
Estimating prediction error (qualitative outcome)
- The premise is the same as cross valiation for quantitative outcomes
- Split the data into K parts, where \(C_1, C_2, \dots, C_k\) indicate the indices of observations in part \(k\)
$$CV_K = \sum_{k=1}^K\frac{n_k}{n}Err_k$$
- \(Err_k = \sum_{i\in C_k}I(y_i\neq\hat{y}_i)/n_k\) (missclassification rate)
- \(n_k\) is the number of observations in group \(k\)
- \(\hat{y}_i\) is the fit for observation \(i\) obtained from the data with the part \(k\) removed
CV
- Go to the sta-363-s20 GitHub organization and search for
appex-03-cv - Clone this repository into RStudio Cloud
- Complete the exercises
- Remember to knit, commit, push!