Non-linearity
Dr. D’Agostino McGowan
Non-linear relationships
What have we used so far to deal with non-linear relationships?
Non-linear relationships
What have we used so far to deal with non-linear relationships?
- Hint: What did you use in Lab 03?
Non-linear relationships
What have we used so far to deal with non-linear relationships?
- Hint: What did you use in Lab 03?
- Polynomials!
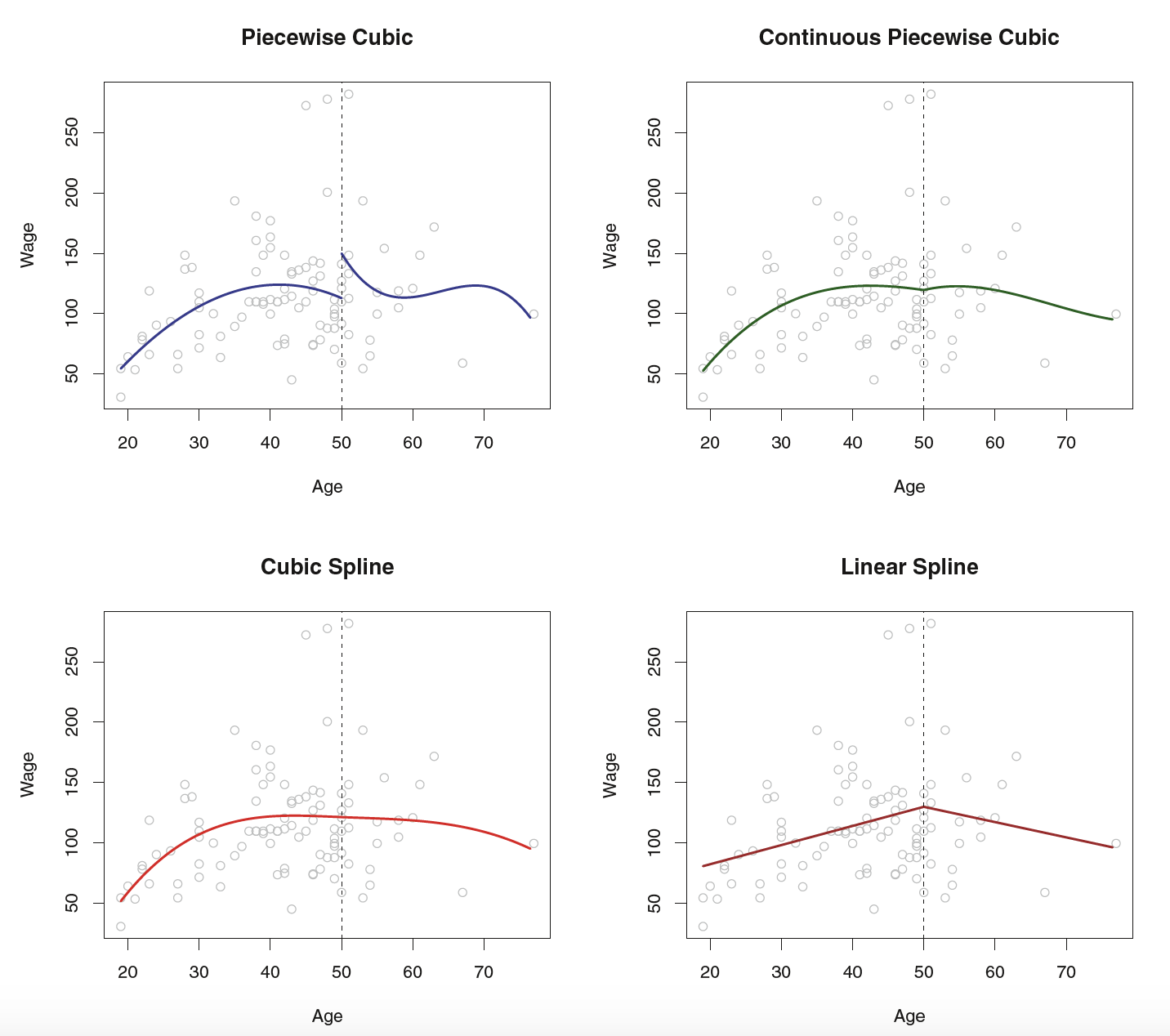
Polynomials
yi=β0+β1xi+β2x2i+β3x3i⋯+βdxdi+ϵi
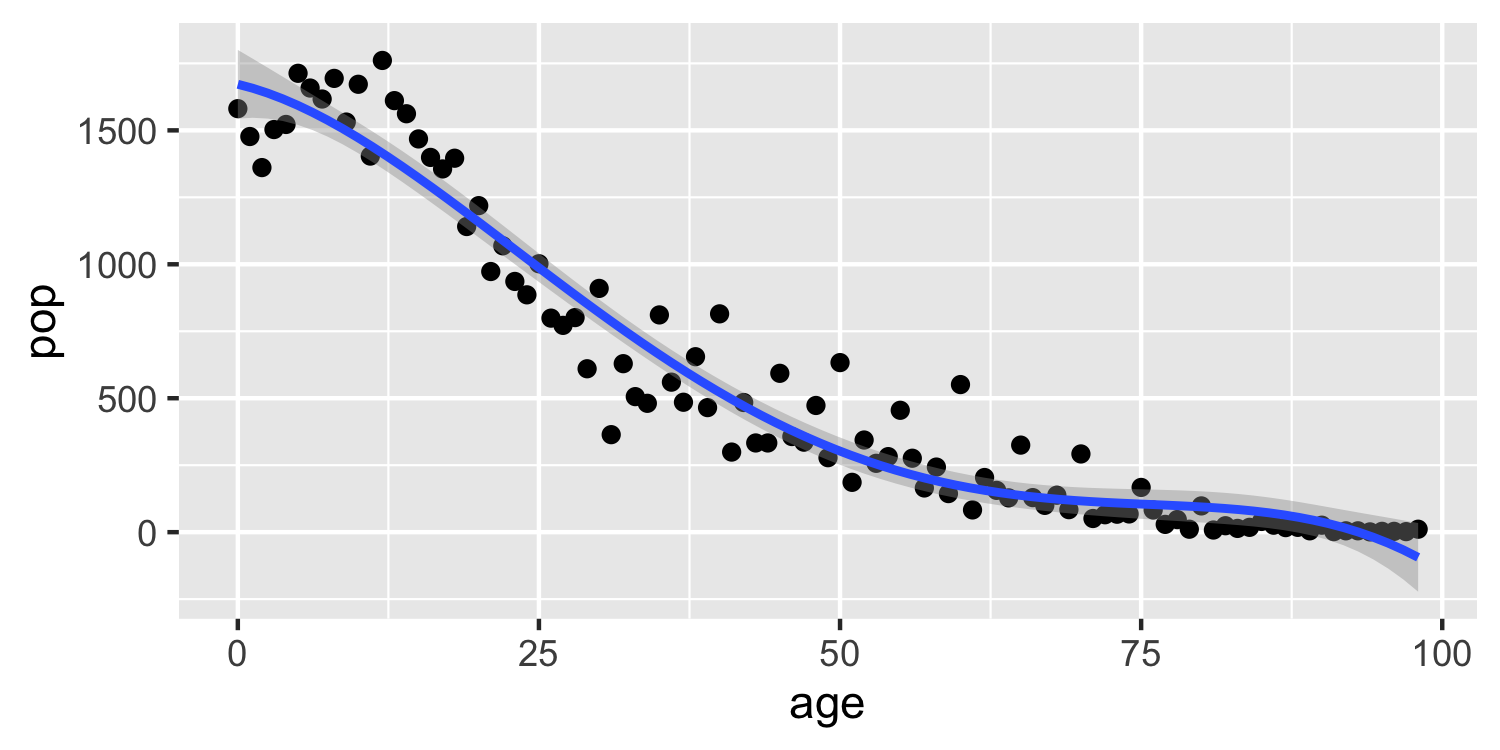
Polynomials
yi=β0+β1xi+β2x2i+β3x3i⋯+βdxdi+ϵi

- This is data from the Columbia World Fertility Survey (1975-76) to examine household compositions
Polynomials
yi=β0+β1xi+β2x2i+β3x3i⋯+βdxdi+ϵi

- This is data from the Columbia World Fertility Survey (1975-76) to examine household compositions
- Fit here with a 4th degree polynomial
How is it done?
- New variables are created ( X1=X, X2=X2, X3=X3, etc) and treated as multiple linear regression
How is it done?
- New variables are created ( X1=X, X2=X2, X3=X3, etc) and treated as multiple linear regression
- We are not interested in the individual coefficients, we are interested in how a specific x value behaves
^f(x0)=^β0+^β1x0+^β2x20+^β3x30+^β4x40
How is it done?
- New variables are created ( X1=X, X2=X2, X3=X3, etc) and treated as multiple linear regression
- We are not interested in the individual coefficients, we are interested in how a specific x value behaves
^f(x0)=^β0+^β1x0+^β2x20+^β3x30+^β4x40
- or more often a change between two values, a and b
^f(b)−^f(a)=^β1b+^β2b2+^β3b3+^β4b4−^β1a−^β2a2−^β3a3−^β4a4
How is it done?
- New variables are created ( X1=X, X2=X2, X3=X3, etc) and treated as multiple linear regression
- We are not interested in the individual coefficients, we are interested in how a specific x value behaves
^f(x0)=^β0+^β1x0+^β2x20+^β3x30+^β4x40
- or more often a change between two values, a and b
^f(b)−^f(a)=^β1b+^β2b2+^β3b3+^β4b4−^β1a−^β2a2−^β3a3−^β4a4
^f(b)−^f(a)=^β1(b−a)+^β2(b2−a2)+^β3(b3−a3)+^β4(b4−a4)
Polynomial Regression
^f(b)−^f(a)=^β1(b−a)+^β2(b2−a2)+^β3(b3−a3)+^β4(b4−a4)
How do you pick a and b?
Polynomial Regression
^f(b)−^f(a)=^β1(b−a)+^β2(b2−a2)+^β3(b3−a3)+^β4(b4−a4)
How do you pick a and b?
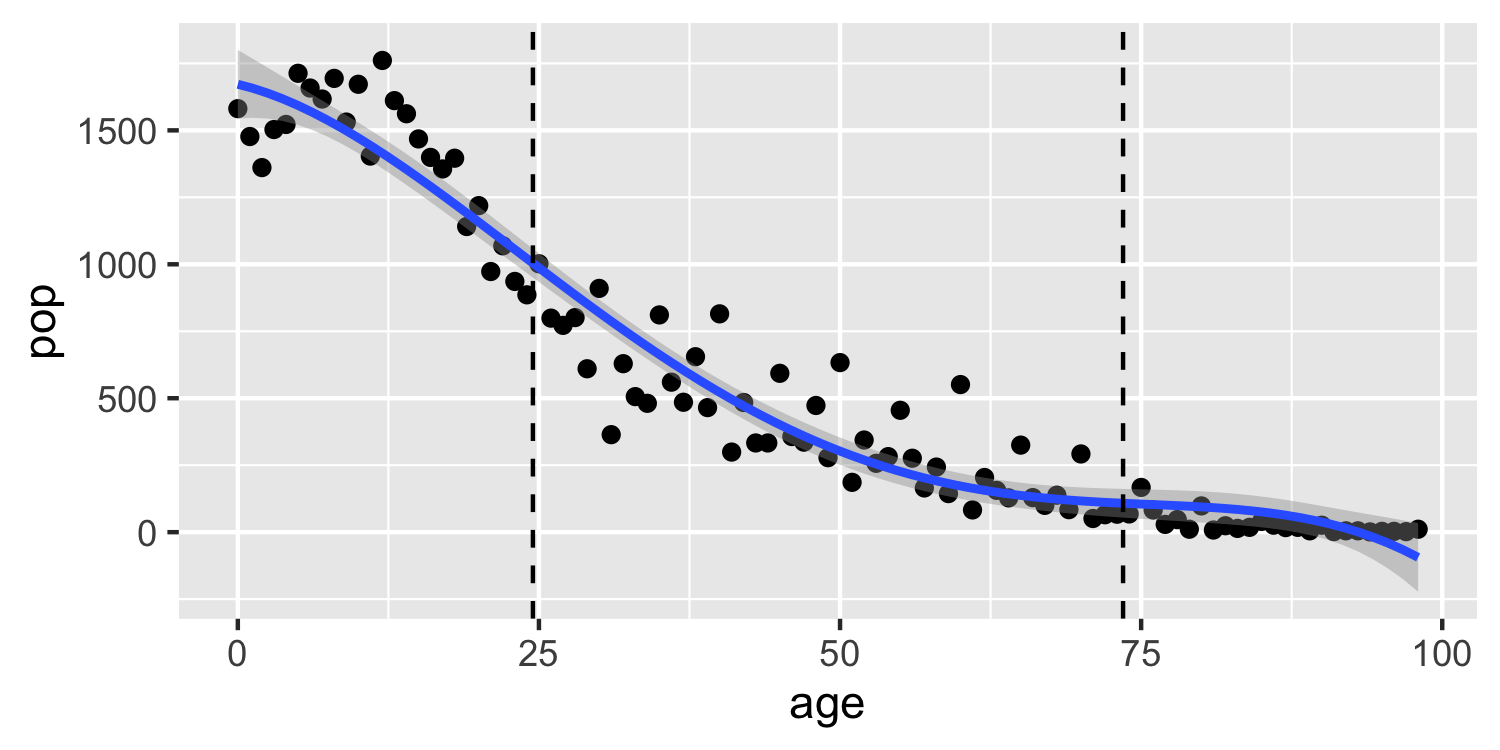
- If given no other information, a sensible choice may be the 25th and 75th percentiles of x
Polynomial Regression
03:00
Polynomial Regression
pop=β0+β1age+β2age2+β3age3+β4age4+ϵ
Using the information below, write out the equation to predicted change in population from a change in age from the 25th percentile (24.5) to a 75th percentile (73.5).
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 1672.0854 | 64.5606 | 25.8995 | 0.0000 |
| age | -10.6429 | 9.2268 | -1.1535 | 0.2516 |
| I(age^2) | -1.1427 | 0.3857 | -2.9627 | 0.0039 |
| I(age^3) | 0.0216 | 0.0059 | 3.6498 | 0.0004 |
| I(age^4) | -0.0001 | 0.0000 | -3.6540 | 0.0004 |
Choosing d
yi=β0+β1xi+β2x2i+β3x3i⋯+βdxdi+ϵi
Either:
- Pre-specify d (before looking 👀 at your data!)
- Use cross-validation to pick d
Choosing d
yi=β0+β1xi+β2x2i+β3x3i⋯+βdxdi+ϵi
Either:
- Pre-specify d (before looking 👀 at your data!)
- Use cross-validation to pick d
Why?
Polynomial Regression
- polynomials have notoriously bad tail behavior (so they can be bad for extrapolation)
Polynomial Regression
- polynomials have notoriously bad tail behavior (so they can be bad for extrapolation)
What does this mean?
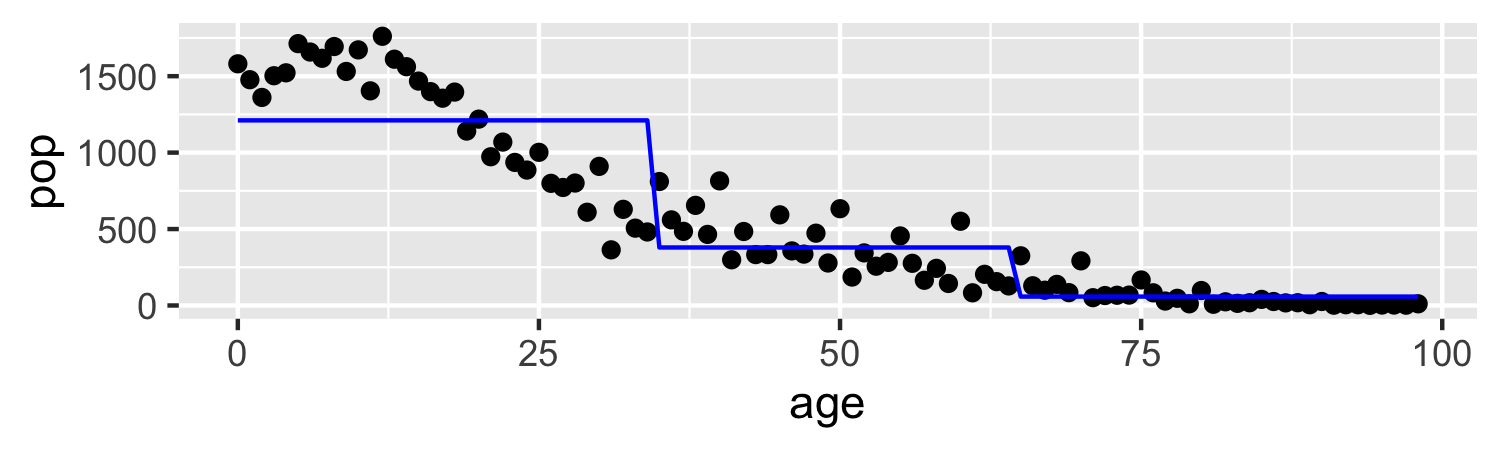
Step functions
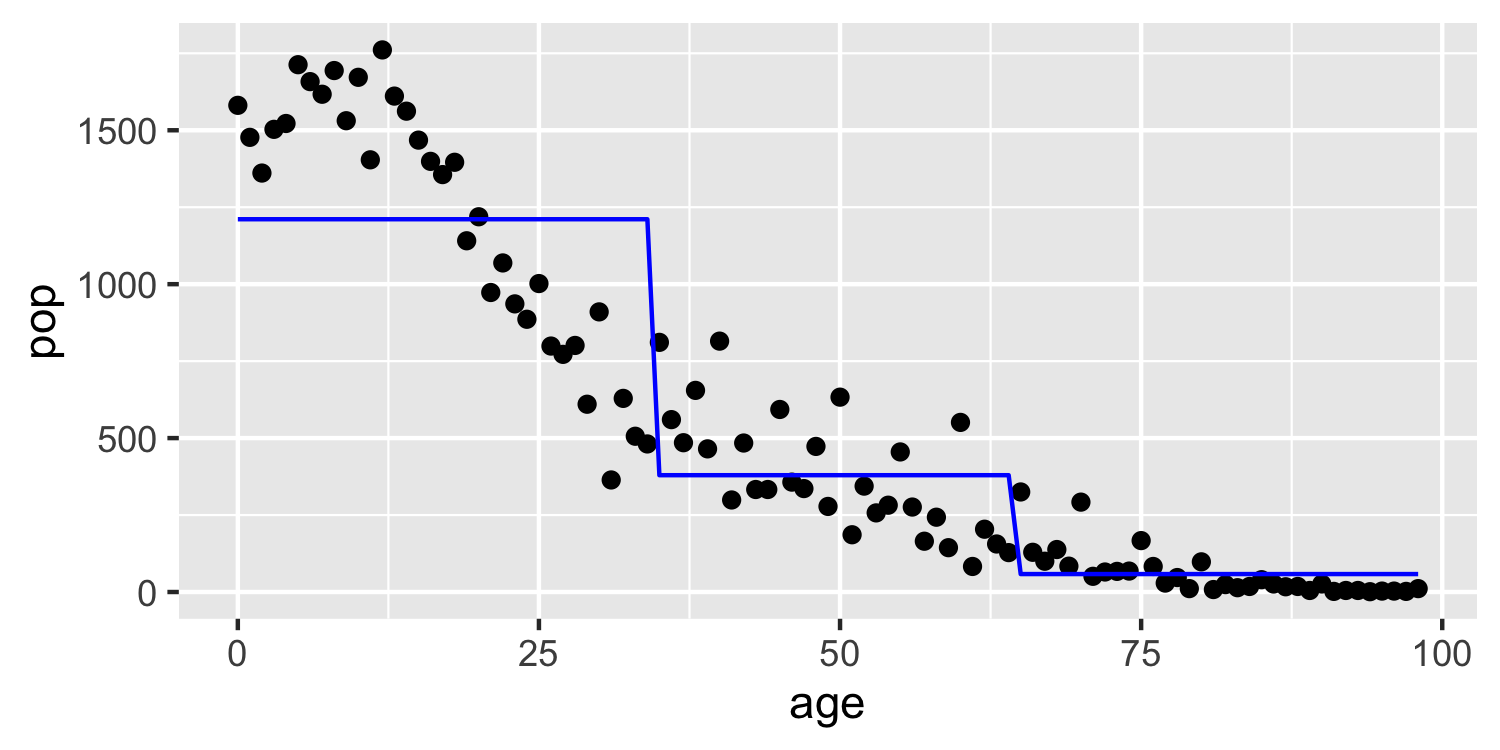
- Another way to create a transformation is to cut the variable into distinct regions
C1(X)=I(X<35),C2(X)=I(35≤X<65),C3(X)=I(X≥65)
Step functions
- Create dummy variables for each group
Step functions
- Create dummy variables for each group
- Include each of these variables in multiple regression
Step functions
- Create dummy variables for each group
- Include each of these variables in multiple regression
- The choice of cutpoints or knots can be problematic (and make a big difference!)
Step functions
C1(X)=I(X<35),C2(X)=I(35≤X<65),C3(X)=I(X≥65)
Step functions
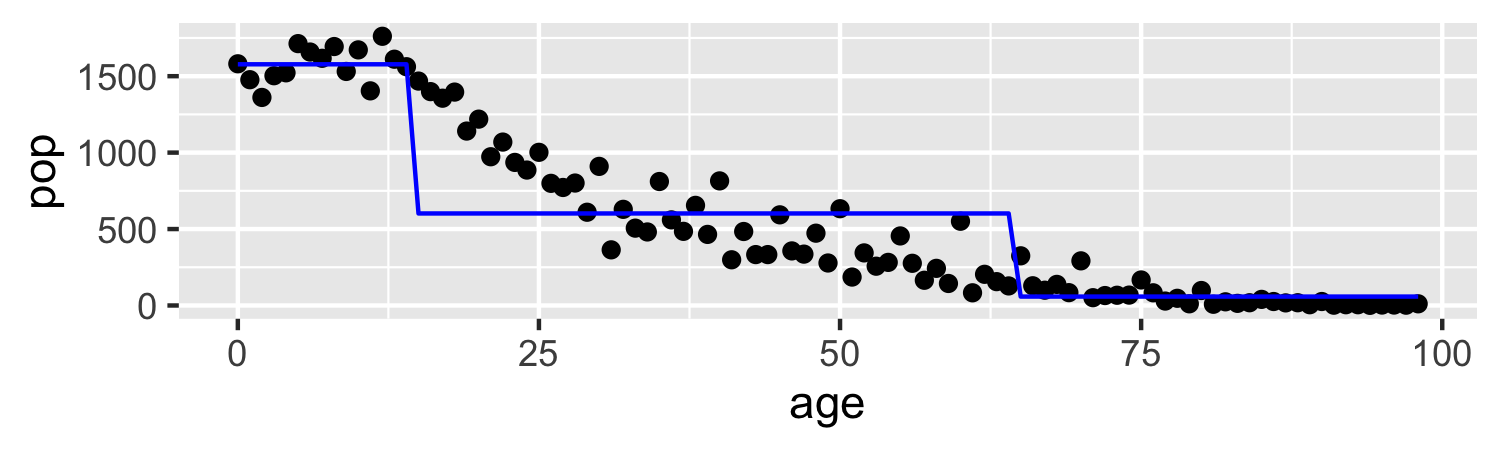
C1(X)=I(X<35),C2(X)=I(35≤X<65),C3(X)=I(X≥65)

C1(X)=I(X<15),C2(X)=I(15≤X<65),C3(X)=I(X≥65)
Piecewise polynomials
- Instead of a single polynomial in X over it's whole domain, we can use different polynomials in regions defined by knots
yi={β01+β11xi+β21x2i+β31x3i+ϵiif xi<cβ02+β12xi+β22x2i+β32x3i+ϵiif xi≥c
Piecewise polynomials
- Instead of a single polynomial in X over it's whole domain, we can use different polynomials in regions defined by knots
yi={β01+β11xi+β21x2i+β31x3i+ϵiif xi<cβ02+β12xi+β22x2i+β32x3i+ϵiif xi≥c
What could go wrong here?
Piecewise polynomials
- Instead of a single polynomial in X over it's whole domain, we can use different polynomials in regions defined by knots
yi={β01+β11xi+β21x2i+β31x3i+ϵiif xi<cβ02+β12xi+β22x2i+β32x3i+ϵiif xi≥c
What could go wrong here?
- It would be nice to have constraints (like continuity!)
Piecewise polynomials
- Instead of a single polynomial in X over it's whole domain, we can use different polynomials in regions defined by knots
yi={β01+β11xi+β21x2i+β31x3i+ϵiif xi<cβ02+β12xi+β22x2i+β32x3i+ϵiif xi≥c
What could go wrong here?
- It would be nice to have constraints (like continuity!)
- Insert splines!
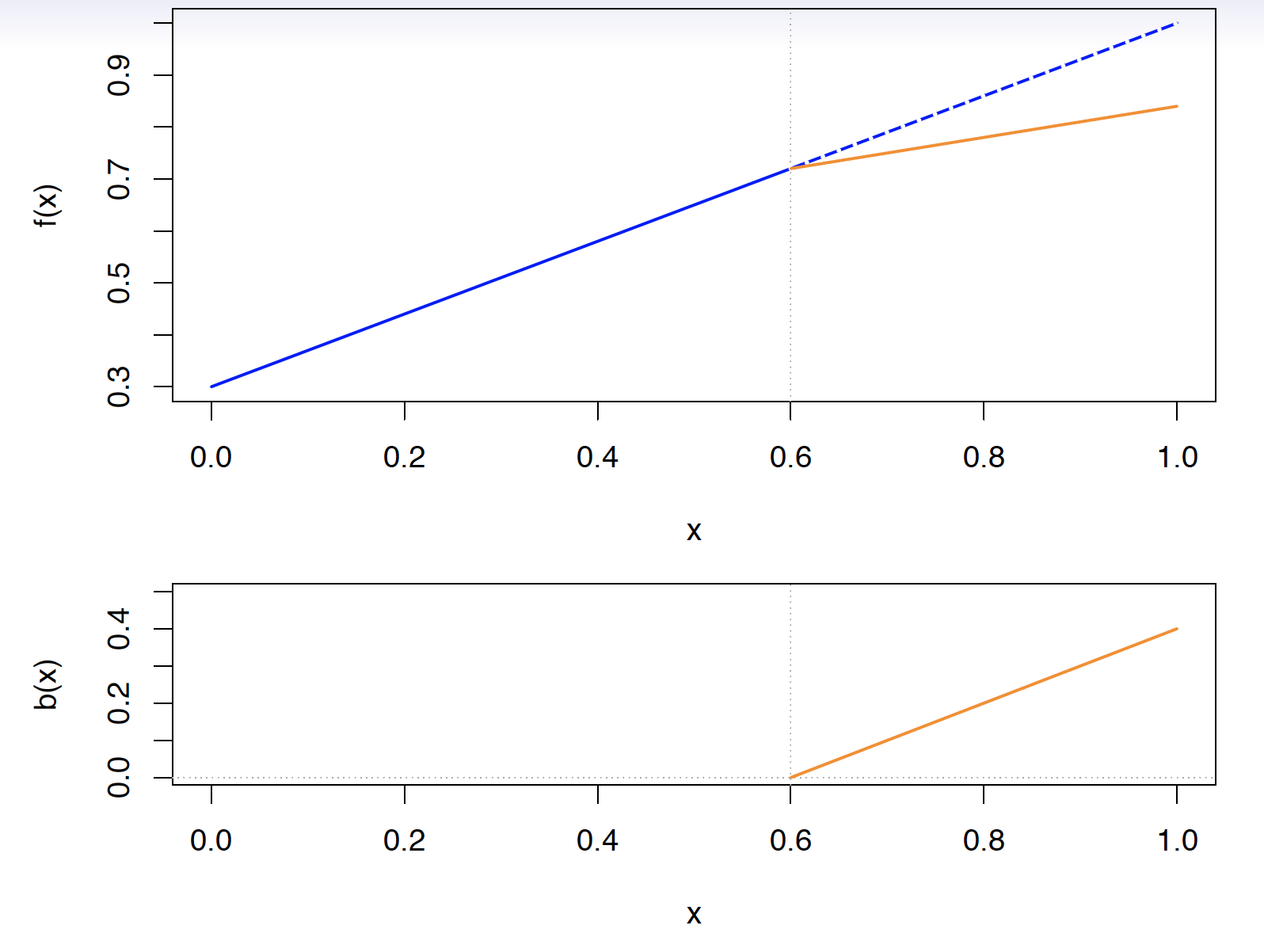
Linear Splines
A linear spline with knots at ξk, k=1,…,K is a piecewise linear polynomial continuous at each knot
Linear Splines
A linear spline with knots at ξk, k=1,…,K is a piecewise linear polynomial continuous at each knot
yi=β0+β1b1(xi)+β2b2(xi)+⋯+βK+1bK+1(xi)+ϵi
Linear Splines
A linear spline with knots at ξk, k=1,…,K is a piecewise linear polynomial continuous at each knot
yi=β0+β1b1(xi)+β2b2(xi)+⋯+βK+1bK+1(xi)+ϵi
- bk are basis functions
b1(xi)=xibk+1(xi)=(xi−ξk)+,k=1,…,K
Linear Splines
A linear spline with knots at ξk, k=1,…,K is a piecewise linear polynomial continuous at each knot
yi=β0+β1b1(xi)+β2b2(xi)+⋯+βK+1bK+1(xi)+ϵi
- bk are basis functions
b1(xi)=xibk+1(xi)=(xi−ξk)+,k=1,…,K
Here ()+ means the positive part
(xi−ξk)+={xi−ξkif xi>ξk0otherwise
Cubic Splines
A cubic spliens with knots at ξi,k=1,…,K is a piecewise cubic polynomial with continuous derivatives up to order 2 at each knot.
Cubic Splines
A cubic spliens with knots at ξi,k=1,…,K is a piecewise cubic polynomial with continuous derivatives up to order 2 at each knot.
Again we can represent this model with truncated power functions
yi=β0+β1b1(xi)+β2b2(xi)+⋯+βK+3bK+3(xi)+ϵi
b1(xi)=xib2(xi)=x2ib3(xi)=x3ibk+3(xi)=(xi−ξk)3+,k=1,…,K
Cubic Splines
A cubic spliens with knots at ξi,k=1,…,K is a piecewise cubic polynomial with continuous derivatives up to order 2 at each knot.
Again we can represent this model with truncated power functions
yi=β0+β1b1(xi)+β2b2(xi)+⋯+βK+3bK+3(xi)+ϵi
b1(xi)=xib2(xi)=x2ib3(xi)=x3ibk+3(xi)=(xi−ξk)3+,k=1,…,K
where
(xi−ξk)3+={(xi−ξk)3if xi>ξk0otherwise
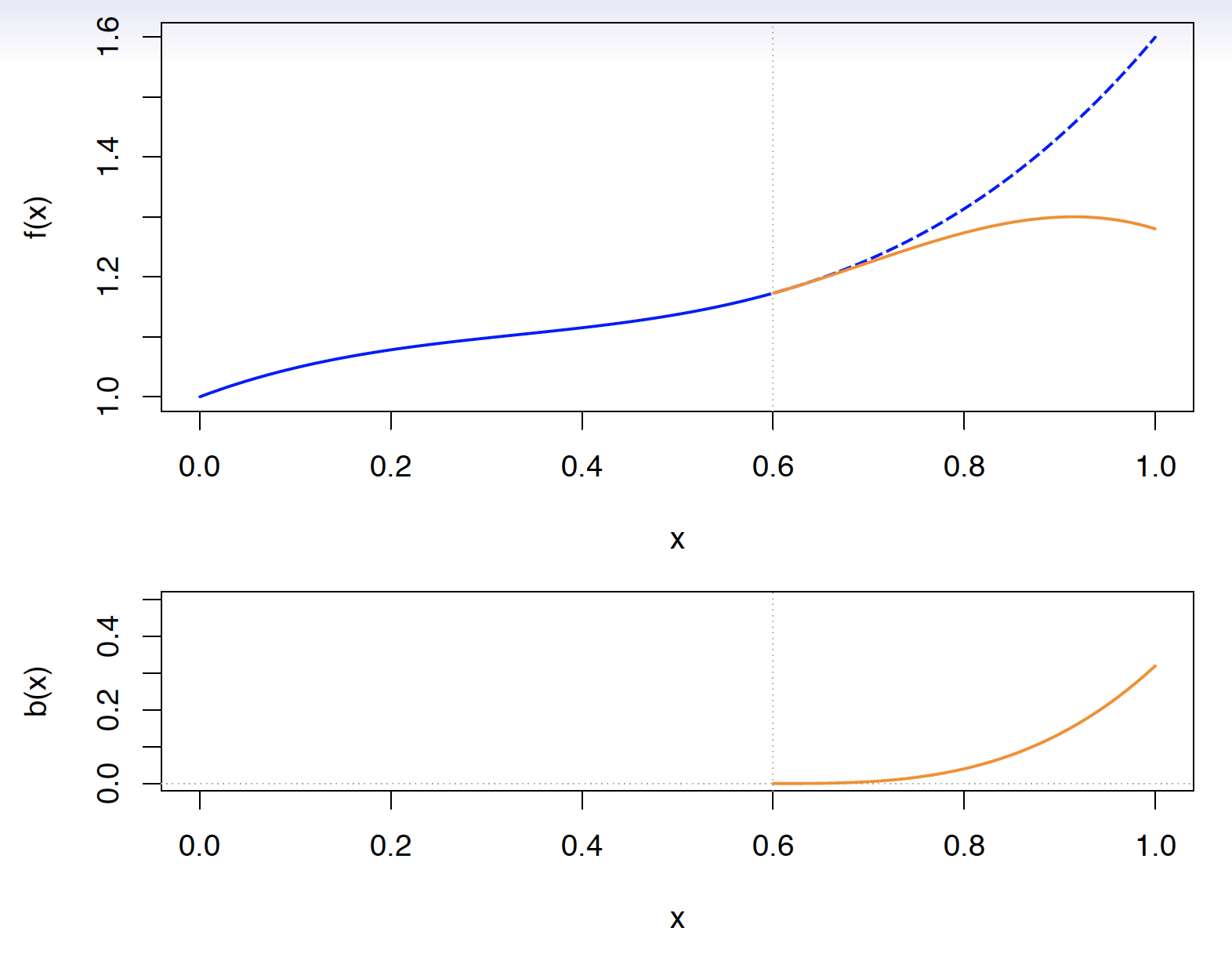
Natural cubic splines
A natural cubic spline extrapolates linearly beyond the boundary knots
Natural cubic splines
A natural cubic spline extrapolates linearly beyond the boundary knots
- This adds 4 extra constraints and allows us to put more internal knots for the same degrees of freedom as a regular cubic spline
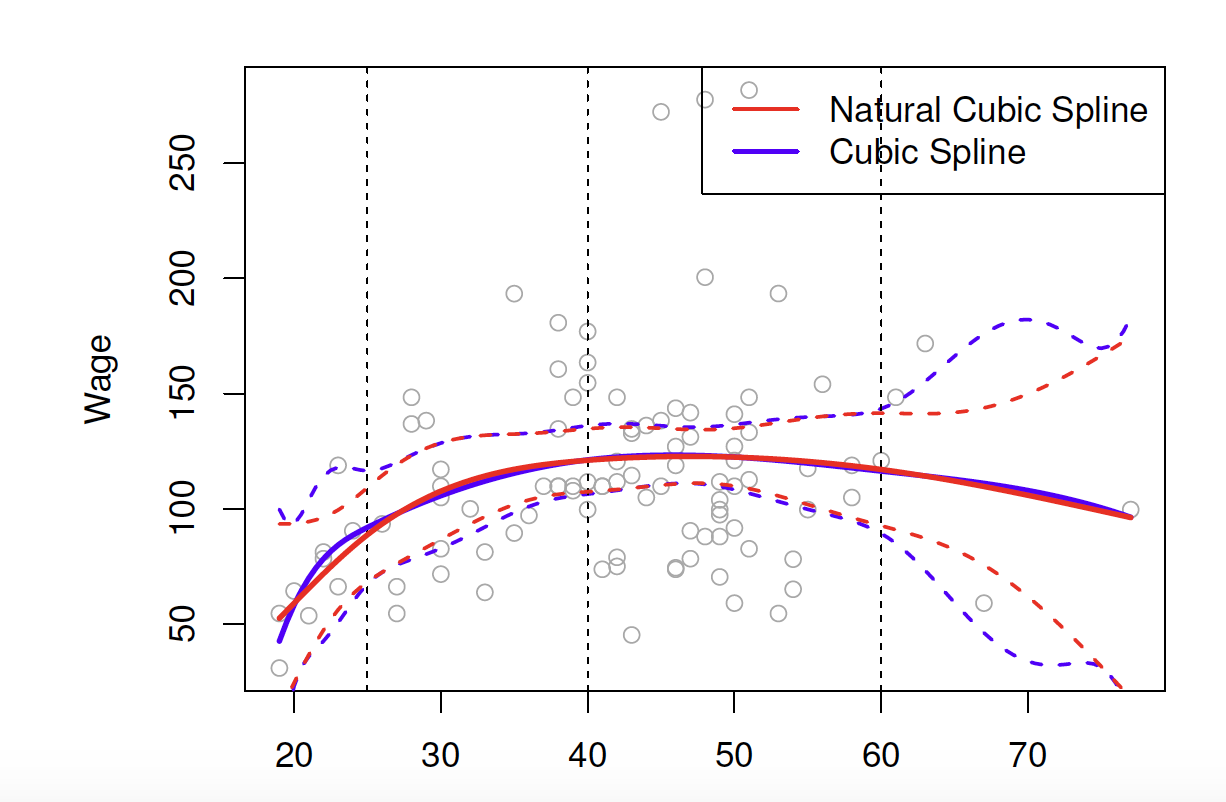
Knot placement
- One strategy is to decide K (the number of knots) in advance and then place them at appropriate quantiles of the observed X
Knot placement
- One strategy is to decide K (the number of knots) in advance and then place them at appropriate quantiles of the observed X
- A cubic spline with K knots has K+4 parameters (or degrees of freedom!)
Knot placement
- One strategy is to decide K (the number of knots) in advance and then place them at appropriate quantiles of the observed X
- A cubic spline with K knots has K+4 parameters (or degrees of freedom!)
- A natural spline with K knots has K degrees of freedom
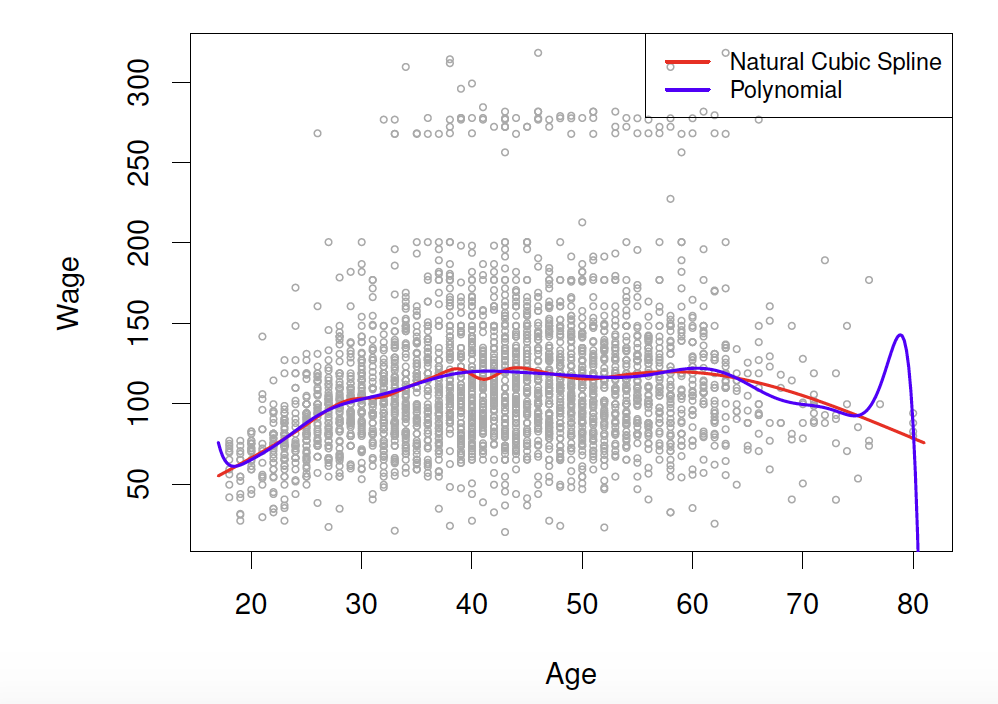
Knot placement
- Here is a comparision of a degree-14 polynomial and natural cubic spline (both have 15 degrees of freedom)